You can see the slides for all of the talks at the workshop I was just at in Paris, including the three talks I gave. (As I said in my last post, this was a pretty specialized workshop, so you probably don’t want to unless you’re a researcher who works on the microwave background.)
Author: Ted Bunn
I am chair of the physics department at the University of Richmond. In addition to teaching a variety of undergraduate physics courses, I work on a variety of research projects in cosmology, the study of the origin, structure, and evolution of the Universe. University of Richmond undergraduates are involved in all aspects of this research. If you want to know more about my research, ask me!
Bonjour!
I’m spending this week in Paris, at a conference on Bolometric interferometry for the B mode search. This is a narrowly focused workshop on a specific technique that may be used for future measurements of the microwave background. (That’s why its name is so completely esoteric.) For a number of years now, I’ve been part of a collaboration trying to develop this technique.
This is the second conference I’ve been to in the past few weeks. St. Louis was perfectly nice, but I have to say it’s nicer to be in Paris, weak dollar notwithstanding.
Plutoids
According to the International Astronomical Union, Pluto is still not a planet, but it is a Plutoid. If I recall correctly, at the time the original naming decision was made, there was a proposal to call the class of Pluto-like objects “Plutons,” but that was rejected, in part because “Pluton” is already the name of Pluto in various languages, including French. I guess “Plutoid” solves that problem.
I don’t much care about Pluto no longer being considered a planet, but I do think that the IAU made a poor choice of naming conventions. According to the new system, Pluto and similar objects are not planets, but they are “dwarf planets.” That’s right: a dwarf planet is not a planet. That’s a needlessly confusing naming convention, especially since it’s inconsistent with the terminology in the rest of astronomy: dwarf stars are stars, and dwarf galaxies are galaxies.
That’s old news now, of course: the new wrinkle, namely the introduction of the term “Plutoid,” neither solves nor worsens that problem.
Even though it’s all in the past, here are a couple of observations about the Pluto-classification flap:
1. Obviously, no interesting scientific questions hinge on whether we choose to classify Pluto as a planet. I recall a news article at the time of the Great Naming Controversy saying that the future of NASA’s New Horizons probe was in doubt because of the reclassification of Pluto as a non-planet. That’s an obviously ridiculous notion: As Abraham Lincoln could tell you, the nature of a thing doesn’t change because of what we call it.
2. The justification for the Great Renaming was to have a precise physical definition of the word “planet.” Mike Brown has argued against the need for such a definition: Why not just consider the word “planet” to mean the nine bodies that it has traditionally meant? By way of analogy, the word “continent” refers to a conventional set of seven land masses. We don’t really need to justify why it’s that list of seven (Why aren’t Europe and Asia considered as one? Why not include Greenland?). Often, science needs precise, objective definitions in order to proceed. But it’s not clear that in this case anyone was being hampered by the arbitrary nine-body definition of the word “planet.” What, exactly, was the problem that the IAU solved?
American Astronomical Society Meeting
My research group and I are just back from the summer AAS meeting in St. Louis. Here we all are at the hotel just before leaving:
Our group presented four posters, with primary authors Austin Bourdon, Brent Follin, Ben Rybolt, and me. This means that pretty large fraction of the undergraduate presentations were by UR students. I suspect that we had more undergraduates presenting than any other college, although someone said that Wesleyan had a lot too. If you want to know about the research we were presenting, take a look at Austin’s, Brent’s, Ben’s, and my posters.
The fifth member of the group is Haoxuan Jeff Zheng, who wasn’t presenting this time because he only started research quite recently.
The meeting felt a bit small to me, compared to past AAS meetings I’ve been to: there didn’t seem to be that much going on. There were certainly some good talks, though. John Monnier talked about using interferometers (particularly CHARA) to produce images of rapidly rotating stars. In general, stars just look like points of light, even through the largest telescopes. But with these interferometers, you can actually resolve the stars well enough to see their overall shapes. Rapidly rotating stars bulge out at the equator, so they’re quite far from circular in appearance. Some are rotating so fast that they’re pretty close to breaking up. I had no idea how far the state of the art in this field had advanced in recent years.
The best talk was by Sean Carroll, on one of those questions that sounds stupid when you first hear it, but gets more interesting the more you think about it: Why does time flow in one direction and not the other? Why is the future different from the past? The reason it’s puzzling is that the microscopic laws of physics look the same whether you run time forwards or backwards, which makes it a bit strange that the large-scale universe doesn’t.
A conventional answer to this question is to invoke the second law of thermodynamics. Carroll argued that this only pushes the problem back one step, rather than really solving it. He argued further that none of the usual attempts at further explanation, including the theory of inflation, really solve the problem. He speculated a bit on what a true explanation might look like, but mostly had to admit that we have no idea.
Galileo
Apparently there’s a tradition here at the University of Richmond: when a faculty member gets tenured, he or she chooses a book for the library and writes a description of the importance of the book. The library inserts that description into the catalog, or into the book, or something like that.
Since I just got tenure, I had to choose a book to write about. After thinking about it for a while, I decided to go with Galileo’s Dialogue concerning the two chief world systems. Here’s the description I’m sending off to the library.
By the way, I really mean it when I say in here that the book is extremely readable. I can’t think of any other book that’s (a) anywhere near as important as this one and (b) actually fun to read. If you haven’t read it, check it out! (Although if you’re at UR, you’ll have to wait a week or so to get it out of the library, because I’ve got it at the moment.)
Anyway, here’s what I wrote:
The central idea of astrophysics is that the same laws of nature we discover in labs on Earth can be used throughout the Universe: there are not separate laws for heavenly bodies. It would be hard to overstate the importance of this insight to the emergence of modern science. Galileo did not invent this idea – like most really big ideas, this one cannot be attributed to any one person. But he deserves a large share of the credit for developing the idea and for persuasively and cogently championing it. Galileo is an all-too-rare figure among the giants of science: he wrote with clarity and even wit for an audience of non-specialists. He wrote in the common language, not in Latin, in a style that makes his work still readable and even enjoyable today.
Galileo has a lot in common with Einstein, so it is fitting that Einstein wrote the foreword to this English translation. In particular, Galileo's description of experiments performed below decks on a moving ship is the direct ancestor of Einstein's discovery of relativity, both in the scientific content of the ideas and in the ingenious use of thought experiments.
Einstein and me
I never met Einstein, which is not surprising, since he died over 20 years before I was born. [Update: Make that 12 years. See Matt Trawick’s comment below.] (The most famous physicists I have ever met, I think, are Eugene Wigner and John Wheeler, who are not exactly household names to non-scientists.) But back when I was in college I did get to know an old friend of Einstein’s pretty well.
Her name was Gabrielle Oppenheim, and she was about 95 when I knew her in the summer of 1988. Because her eyesight was very poor, she hired students to read the newspaper to her. This was a great job, which was passed on from student to student. I don’t remember how much it paid; I would have done it for nothing.
Mrs. Oppenheim told me lots of stories about Einstein. She first met him at a party in Brussels in 1911. Her husband pointed Einstein out and said, “That man will be one of the greatest physicists.” Mrs. Oppenheim’s response: “So I gave him one sandwich more.” (She later told this story to F. Murray Abraham in a Nova documentary, but I heard it first.)
She also said she was with Einstein in 1919 when he got the telegram from Sir Arthur Eddington, announcing that his observations of the bending of starlight had confirmed Einstein’s theory of general relativity. This was the event that made Einstein world-famous. But according to Mrs. Oppenheim, Einstein was much less excited about the result than the other people who were there at the time, because he had never doubted what the result would be.
She knew Einstein in Europe, but she spent much more time with him later in the U.S., when she and her husband had come to Princeton. (Her husband, Paul Oppenheim, was a philosopher.) Once, she and her husband were sailing with Einstein when the boat capsized. Her husband said, “Well, at least if we die with Einstein, we’ll be famous.”
She told me lots of other good stories. Once, she said, she was at a dinner party somewhere in Europe during World War I. A German army officer asked where she was from, and she told him she was Belgian. He replied that Germany would be invading Belgium soon. Mrs. Oppenheim said, “I was so offended by that, that I turned away and didn’t speak to him for the rest of the dinner.”
Mrs. Oppenheim told me way back then that I was “the scientist type”. Given that she hobnobbed with some of the greatest physicists of the 20th century (Bohr and others as well as Einstein), I figured she must know what she was talking about.
And still more on electability
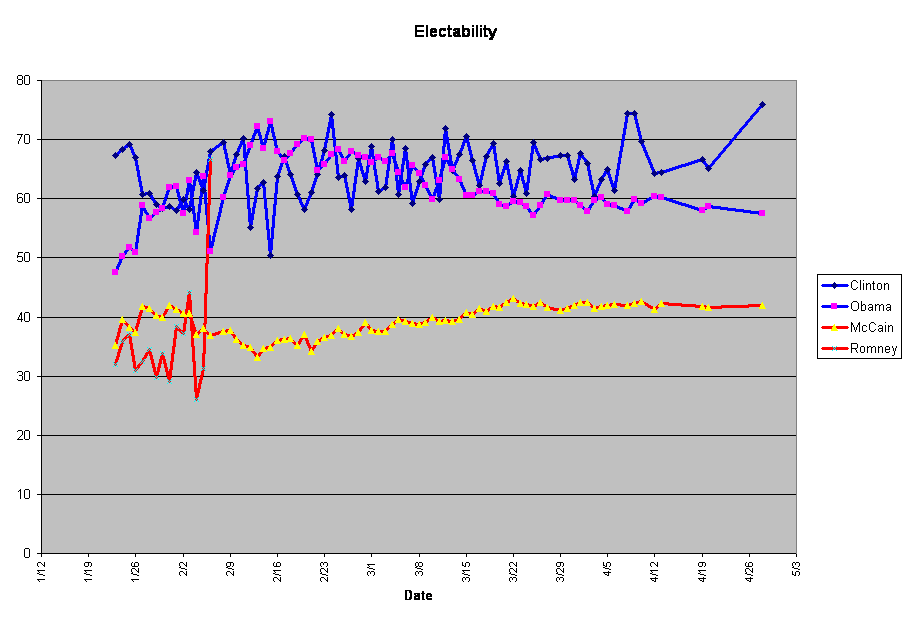
Here’s the latest data on the electability of the Democratic presidential candidates, as determined by the political futures market Intrade.
Probability of getting nomination Probability of winning election Electability
Clinton 17.1% 13% 76%
Obama 80.1% 46% 57.4%
Remember that electability is defined to be the probability that a candidate wins the election, given that the candidate gets the nomination. Intrade lets people bet on which candidate will get the nomination and on which candidate will win the election. In both cases, the odds can be interpreted as probabilities, which are the numbers listed above. The ratio of the probabilities, by Bayes’s Theorem, is the electability.
At the bottom of this post I’ll put a graph showing electability over time. The market “thinks” that Clinton is significantly more electable than Obama, and it has thought so pretty much all the time for the past couple of months.
From conversations with various people it’s become clear that I should be more explicit about what it even means to say what the market thinks a candidate’s electability is. Here’s one way to put it: If you think that Obama’s electability is significantly different from the above value, then you can place bets on Intrade whose odds favor you, and similarly for Clinton. After the page break below, I’ll give excruciatingly explicit details about how you’d place these bets.
Lots of people are confident that the futures market has gotten this wrong — in particular, partisans of each of the two Democrats seem to think that the other one’s electability is very low. A natural question to ask these people is this: have you put your money where your mouth is?
OK. Here’s the electability graph. Data were taken from Slate’s Political Futures pages on every day when I remembered to do it.
Will physics destroy the world?
Apparently a couple of guys are suing to stop the Large Hadron Collider, the new particle accelerator being built at CERN. They’re worried about the possibility that the collisions will produce something like miniature black holes or other exotic objects that would then destroy the Earth.
This sort of worry has come up a bunch of times before. Sometimes the worry is about the possibility that the state of matter that we know and love is only a metastable state, not the most stable state. The idea then would be that, if you produce a single nugget of the true stable state, everything else would collapse into that new state. It’d be like having a supersaturated sugar solution: as soon as you give it a nucleation point, everything crystallizes out. Think Vonnegut’s ice-nine.
So should we be worried about the LHC destroying the world? The short answer is no. This sort of thing is logically possible, so it’s certainly worth considering the possibility, given the enormous downside of destroying the world. But people have considered it very carefully and have shown quite convincingly that there is no risk. There’s a short overview here, with links to the technical reports.
There’s one argument that dispenses with a lot of the various doomsday scenarios. The sorts of collisions that will happen in the LHC happen regularly in the Earth’s upper atmosphere, as ultra-high-energy cosmic rays strike the Earth. You can work out that, over the Earth’s 5-billion-year history, the number of times these events have occurred naturally is many times larger than the number of times they will occur at the LHC. So the fact that the Earth is still around is very strong evidence that this sort of catastrophic scenario is impossible.
As the NY Times article points out, there’s a loophole in this argument. The collisions in the upper atmosphere are fast-moving particles colliding with particles that are essentially at rest. Because of conservation of momentum, anything produced in such a collision would be moving at close to the speed of light, so it wouldn’t stick around long enough to do any damage. In contrast, the collisions in the collider will be of particles moving in opposite directions with essentially equal speeds, so the resulting detritus will be produced nearly at rest. There is a big difference between a micro-black hole whizzing through the Earth at nearly the speed of light, which would have essentially no effect, and one that’s moving slow enough to stick around. To see why you still shouldn’t worry, you have to read the technical reports.
Animal magnetism
I really liked this article in Physics Today about how animals sense magnetic fields. I had no idea that (a) so many different kinds of animals can do it, or (b) so little is known about how they do it.
A yard of snow
This post on the nominal illusion, in which the units of measure we use affect our psychological perception of a quantity, reminded me of something else interesting about the way we perceive units.
When I was in college, my roommate told me about a skiing trip he’d been on, where the snow was “a yard deep.” He’s European, so naturally he was thinking “a meter deep” and converting it for my American ears. To any native speaker of American English, of course, that sounds all wrong: we would say “three feet deep.” The question is why?
As far as I can tell, the answer is that yards are units of horizontal measure, not vertical measure. It’s a bit funny that we have units of length that are only used in certain directions, but once you start looking out for them, there are actually a bunch of them. Miles are horizontal (the exceptions are “the mile-high city” and “the mile-high club,” but I think that in both cases the “incorrect” unit is being deliberately used to make the phrase sound funny or memorable). In aviation, feet are vertical. In the ocean, fathoms are vertical and leagues are horizontal (before saying that “20,000 Leagues Under the Sea” proves this wrong, check out what the title actually means: it’s not how far down they went; it’s how far across.)
Of course, in our everyday lives, we experience horizontal distances quite differently from vertical distances, so maybe we shouldn’t be too surprised that there are different units of measure for them.
There’s a nice analogy here to the theory of relativity. In relativity, we learn to think about spacetime, as opposed to thinking of space and time separately. In doing this, it’s much easier to use a system of units in which distance and time are equivalent (and the speed of light has the value 1). Maybe some day in the future, when we’re all zipping around at close to the speed of light in our personal spacecraft, we’ll all have a strong intuitive grasp of relativity. It’ll seem perfectly natural to us to use the same units for distance and time, and the fact that people used to use different units for the two will seem quaint and archaic, like fathoms and leagues.
Maybe.
Update: I thought of one more exception to the statement that miles are horizontal: the Byrds song “Eight Miles High.” But I think that’s in the same category as the others. Anyway, they were a bunch of hippie stoners, so who cares what they think?