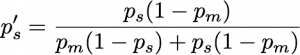Month: February 2012

Apparently the experimenters who found that neutrinos go faster than light have identified some sources of error in their measurements that may explain the result. The word originally went out in an anonymously-sourced blog post over at Science:

According to sources familiar with the experiment, the 60 nanoseconds discrepancy appears to come from a bad connection between a fiber optic cable that connects to the GPS receiver used to correct the timing of the neutrinos’ flight and an electronic card in a computer. After tightening the connection and then measuring the time it takes data to travel the length of the fiber, researchers found that the data arrive 60 nanoseconds earlier than assumed. Since this time is subtracted from the overall time of flight, it appears to explain the early arrival of the neutrinos. New data, however, will be needed to confirm this hypothesis.

Science is of course a very reputable source, but people are rightly skeptical of anonymously sourced information. But apparently it’s legitimate: a statement from the experimental group later confirmed the main idea, albeit in more equivocal language. They say they’ve found two possible sources of error that may eventually prove to explain the result.

Nearly all physicists (probably including the original experimenters) expected something like this to happen: it always seemed far more likely that there was an experimental error of some sort than that revolutionary new physics was occurring. If you asked them why, they’d probably trot out the old saying, “Extraordinary claims require extraordinary evidence,” or maybe the version I prefer, “Never believe an experiment until it has been confirmed by a theory.”

The way to make this intuition precise is with the language of probabilities and Bayesian inference.

Suppose that you hadn’t heard anything about the experimental results, and someone asked you to estimate the probability that neutrinos go faster than light. Your answer would probably be something like 0.000000000000000000000000000000000000000000000000001, but possibly with a lot more zeroes in it. The reason is that a century of incredibly well-tested physics says that neutrinos can’t go faster than light.

We call this number your prior probability. I’ll denote it p_s (s for “superluminal,” which means “faster than light”).

Now suppose that someone asked you for your opinion about the probability that this particular group of experimenters would make a mistake in an experiment like this. (Let’s say that you still don’t know the result of the experiment yet.) I’ll call your answer p_m (m for “mistake”, of course). Your answer will depend on what you know about the experimenters, among other things. They’re a very successful and reputable bunch of physicists, so p_m will probably be a pretty low number, but these experiments are hard, so even if you have a lot of respect for them it won’t be incredibly low the way p_s is.

Now someone tells you the result: “These guys found that neutrinos go faster than light!” The theory of probability (specifically the part often called “Bayesian inference”) gives a precise prescription for how you will update your subjective probabilities to take this information into account. I’m sure you’re dying to know the formula, so here it is:

 

Here p_s‘ means the final (posterior) probability that neutrinos go faster than light.

For any given values of the two input probabilities, you can work out your final probability. But we can see qualitatively how things are going to go without a tedious calculation. Suppose that you have a lot of respect for the experimenters, so that p_m is small, and that you’re not a crazy person, so that p_s is extremely small (much less than p_m). Then to a good approximation the numerator in that fraction is p_s and the denominator is p_m + p_s, which is pretty much p_m. We end up with

p_s‘ = p_s/p_m .

If, for instance, you thought there was only a one in a thousand chance that the experimenters would make a mistake, then p_s‘ would be 1000 p_s. That is, the experimental result makes it 1000 times more likely that neutrinos go faster than light. But you almost certainly thought that ps was much smaller than 1/1000 to begin with — it was more like 0.0000000000000000000000000000000000001 or something. So even after you bump it up by a factor 1000, it’s still small.

The situation here is exactly the same as a classic example people love to use in explaining probability theory. Suppose you take a test for some rare disease, and the test comes back positive. You know that the test only fails 1 in 1000 times. Does that mean there’s only a 0.1% chance of your being disease-free? No. If the disease is rare (your prior probability of having it was low), then it’s still low even after you get the test result. You would only conclude that you probably had the disease if the failure rate for the test was at least as low as the prior probability that you had the disease.

One sociological note: people who talk about probabilities and statistics a lot tend to sort themselves into Bayesian and non-Bayesian camps. But even those scientists who are fervently anti-Bayesian still believed that the superluminal neutrino experiment was wrong, and even those people were (by and large) not surprised by the recent news of a possible experimental error. I claim that those people were in fact unconsciously using Bayesian inference in assessing the experimental results, and that they do so all the time. There’s simply no other way to reason in the face of uncertain, probabilistic knowledge (i.e., all the time). Whether or not you think of yourself as a Bayesian, you are one.

There’s an old joke about a person who put a horseshoe above his door for good luck. His friend said, “C’mon, you don’t really believe that horseshoes bring good luck, do you?” The man replied, “No, but I hear it works even if you don’t believe in it.” Fortunately, Bayesian inference is the same way.

 

Yesterday I posted a criticism of John Allen Paulos’s blog post asking “Why Don’t Americans Elect Scientists?” I focused on the numbers, arguing that scientists are if anything overrepresented in Congress. But it’s worth stepping back and looking at the bigger question: Why might we want more scientists in Congress?

The usual answer, as far as I can tell, is that technology-related issues are important, so we should have representatives who understand them. As Paulos puts it, “given the complexities of an ever more technologically sophisticated world, the United States could benefit from the participation and example of more scientists in government.”

I guess that’s true, but there are lots of areas in which one might wish for expertise in Congress, and I’m not sure technology’s all that near the top. My wish list might include people with expertise in economics, diplomacy, demography, ethics, sociology, and psychology above technology.

I’m not sure that “scientist” is all that great a proxy for “expert in technology” anyway. Some scientists certainly have such expertise, but many don’t, and many non-scientists do. How good a proxy it is depends in part on what you mean by the word “scientist.” Paulos seems to mean “person with some sort of technical training,” but in that case you should certainly include engineers and doctors, in which case the level of representation in Congress is quite high.

When a scientist says we need more scientists in Congress, I suspect that the real reason is not expertise in technology but some combination of the following:

• Scientists are smart, and we need more smart people in Congress.
• Scientists will be more likely to base policy decisions on analytic, data-based arguments.
• Scientists will be more likely to support increased funding for science.

I’m actually sympathetic to all of these arguments, but let’s remember that not all scientists meet these criteria and plenty of non-scientists do.

 

Various scientists I know have been linking to a NY Times blog post bemoaning the fact that scientists are underrepresented in the US government. The author, John Allen Paulos, is a justly celebrated advocate for numeracy, so you’d expect him to get the numbers right. But as far as I can tell, his central claim is numerically unjustified.

As evidence for this underrepresenation, Paulos writes

Among the 435 members of the House, for example, there are one physicist, one chemist, one microbiologist, six engineers and nearly two dozen representatives with medical training.

To decide if that’s underrepresentation, we have to know what population we’re comparing to. And there are three different categories mentioned here: scientists, engineers, and medical people. Let’s take them in turn.

“Pure” science .

The physicist, chemist, and microbiologist are in fact two people with Ph.D.’s and one with a masters degree.

Two Ph.D. scientists is actually an overrepresentation compared to the US population as a whole. Eyeballing a graph from a Nature article here, there were fewer than 15000 Ph.D.’s per year awarded in the sciences in the US back in the 1980s and 1990s (when most members of Congress were presumably being educated). The age cohort of people in their 50s (which I take to be the typical age of a member of Congress) has about 5 million people per year (this time eyeballing a graph from the US Census). So if all of those Ph.D.’s went to US citizens, about 0.3% of the relevant population has Ph.D.’s in science. A lot of US Ph.D.’s go to foreigners, so the real number is significantly less. Two out of 435 is about 0.45%, so there are too many Ph.D. scientists in Congress.

Presumably more people have masters degrees than Ph.D.’s, so if you define “scientist” as someone with either a masters or a Ph.D. in science, then it might be true that scientists are underrepresented in Congress. I couldn’t quickly find the relevant data on numbers of masters degrees in the sciences. In physics, it’s very few — about as many Ph.D.’s are granted as masters degrees in any given year, according to the American Institute of Physics. But it’s probably more in other disciplines.

So I’m quite prepared to believe that  having 3 out of 435 members of Congress in the category of “people with masters or Ph.D.’s in the sciences” means that that group is underrepresented. But I’m not convinced that that’s an interesting group to talk about. In particular, if you’re trying to count the number of people with some sort of advanced scientific training, it makes no sense to exclude physicians from the count.

Engineers.

The Bureau of Labor Statistics says that there are about 1.6 million engineering jobs in the US. The work force is probably something like 200 million workers, so engineers constitute less than 1% of the work force, but they’re more than 1% of the House (6/435). So engineers are overrepresented too.

Physicians.

Doctors are even more heavily overrepresented: there are about a million doctors in the US, which is about 0.5% of the work force, but “people with medical training” are about 5% of Congress. (Some of those aren’t physicians — for instance, one is a veterinarian — but most are.)

So what?

As a simple statement of fact, it is not true that scientists are underrepresented in Congress. What, then, is Paulos claiming? I can only guess that he intends to make a normative rather than a factual statement (that is, an “ought” rather than an “is”). Scientists are underrepresented in comparison to what he he thinks the number ought to be. Personally, my instinct would be to be sympathetic to such a claim. Unfortunately, he neither states this claim clearly nor provides much of an argument in support of it.

(And I didn’t even know this until yesterday.)

Apparently the NFC has won the coin toss in all of the last 14 Super Bowls. As Sean Carroll points out, there’s a 1 in 8192 chance of 14 coin flips all coming out the same way, which via the usual recipe translates into a 3.8 sigma result. In the standard conventions of particle physics, you could get that published as “evidence for” the coin being unfair, but not as a “detection” of unfairness. (“Detection” generally means 5 sigmas. If I’ve done the math correctly, that requires 22 coin flips.)

But this fact isn’t really as surprising at that 1/8192 figure makes it sound. The problem is that we notice when strange things happen but not when they don’t. There’s a pretty long list of equally strange coin-flip coincidences that could have happened but didn’t:

• The coin comes up heads (or tails) every time
• The team that calls the toss wins (or loses) every time
• The team that wins the toss wins (or loses) the game every time

etc. (Yes, the last one’s not entirely fair: presumably winning the toss confers some small advantage, so you wouldn’t expect 50-50 probabilities. But the advantage is surely small, and I doubt it’d be big enough to have a dramatic effect over a mere 14 flips.)

So the probability of some anomaly happening is many times more than 1/8192.

Incidentally, this sort of problem is at the heart of one of my current research interests. The question is how —  or indeed whether — to explain certain “anomalies” that people have noticed in maps of the cosmic microwave background radiation. The problem is that there’s no good way of telling whether these anomalies need explanation: they could just be chance occurrences that our brains, which have evolved to notice patterns, picked up on. Just think of all the anomalies that could have occurred in the maps but didn’t!

The 14-in-a-row statistic is problematic in another way: it involves going back into the past for precisely 14 years and then stopping. The decision to look at 14 years instead of some other number was made precisely because it yielded a surprising low-probability result. This sort of procedure can lead to very misleading conclusions. It’s more interesting to look at the whole history of the Super Bowl coin toss.

According to one Web site, the NFC has one 31 out of 45 tosses. (I’m too lazy to confirm this myself. I found lists of which team has won the toss over the years, but my ignorance of football prevents me from making use of these lists: I don’t know from memory which teams are NFC and which are AFC, and I didn’t feel like looking them all up.)  That imbalance isn’t as unlikely as 14 in a row: you’d expect an imbalance at least this severe about 1.6% of the time. But that’s well below the 5% p-value that people often use to delimit “statistical significance.” So if you believe all of those newspaper articles that report a statistically significant benefit to such-and-such a medicine, you should believe that the Super Bowl coin toss is rigged.

Contrapositively (people always say “conversely” here, but Mr. Jorgensen, my high school math teacher, would never let me get away with such an error), if you don’t believe that the Super Bowl coin toss is rigged, you should be similarly skeptical about news reports urging you to take resveratrol, or anti-oxidants, or whatever everyone’s talking about these days. (Unless you’re the Tin Man — he definitely should have listened to the advice about anti-oxidants.)

 

In a piece in the Chronicle of Higher Education, and Elsevier spokesperson defends their pricing practices:

“Over the past 10 years, our prices have been in the lowest quartile in the publishing industry,” said Alicia Wise, Elsevier’s director of universal access. “Last year our prices were lower than our competitors’.

It’d be interesting to know what metric they’re using. If you take their entire catalog of journals and average together the subscription prices, you get something like $2500 per year. That is indeed in line with typical academic journal costs. But that average is potentially misleading, since it includes a couple of thousand cheap journals that you probably don’t care about, along with a few very high-impact journals that are priced many times higher. Want Brain Resarch? It’ll cost you $24,000 per year.

Of course, in a free market system, Elsevier is allowed to charge whatever it wants. And I’m allowed to decide whether I want to participate, as a customer and more importantly as a source of free labor (writing and refereeing articles for them).

Of course, even “normal” journal prices seem kind of exorbitant. Authors submit articles for free (and in some cases pay page charges), and referees review them for free. So why do we have to pay thousands of dollars per year to subscribe to a journal? I admit that I don’t understand the economics of scholarly journals at all.

If you’re an academic, you really don’t have much choice about participating in the system, but you do have a choice about where to donate your free labor. I tend to publish in and referee for journals run by the various scholarly professional societies (American Physical Society, American Astronomical Society, Royal Astronomical Society). That way, even if the journals are the sources of exorbitant profits, at least those funds are going toward a nonprofit organization that does things I believe in.