Month: August 2011

Here’s the second puzzle I found in the August AJP, specifically in this article. (I describe the first puzzle in another post.) I’d never seen this one before, and I found the answer to be very counterintuitive.

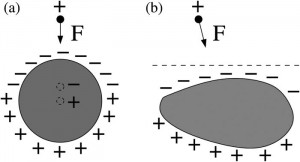
Suppose you have a point charge located somewhere near a perfect conductor with zero net charge. We’re doing good old electrostatics here — nothing’s moving. Intro physics students learn what generically happens in this situation: the presence of the point charge induces negative charge on the near side of the conductor and positive charge on the far side (assuming the point charge is positive). Because the negative charge is closer, you get a net attraction:

Here’s the puzzle: is there any arrangement (i.e., any choice of shape for the conductor and location for the point charge) that leads to a repulsive force between the two?

Figure (b) above shows one way to define “repulsive” more precisely, although pretty much any way will do. Suppose that there is some plane (dashed line in the figure) with the point charge on one side and the whole conductor on the other side. Is there any situation in which the force on the point charge points away from the plane?)

The August 2011 issue of the American Journal of Physics (paywalled, I assume) has two articles about nice physics puzzles. The statement of these puzzles should be understandable to people who know university-level introductory physics, but the solutions are hard.

Here’s the first one. I’ll put the second in another post.

Suppose you have  a strangely-shaped perfectly reflecting cavity like the one in Figure (a) below. The surface consists of parts of two ellipsoids and one sphere. The ellipsoids have foci A and B, and the sphere’s center is at B. Any light ray leaving point A hits part of an ellipsoid and ends up at B. Some light rays leaving B hit ellipsoids and end up at A, while others hit the sphere and go back to B.

Now put objects (blackbodies) at points A and B. They both radiate. All of the radiation from A heats up B, but only some of the radiation from B heats up A. So if the two bodies start out at the same temperature, there’ll be a net energy flow from A to B. But that violates the second law of thermodynamics. What’s going on?

In real life, such a system wouldn’t obey ray optics — the radiation would diffract around, eventually filling the volume of the cavity. Also, the walls wouldn’t really be perfectly reflective, so they’d heat up and radiate themselves. But I don’t think those considerations count as resolutions of the paradox: we can certainly imagine a world in which ray optics works and reflection work perfectly, and the second law should hold in such a world.

Someone told me this puzzle back when I was in grad school, and it bothered me for a while. Eventually, I think I hit on the same answer as the one in the AJP article.