Month: January 2011

On Roger Ebert’s blog, the acclaimed film editor Walter Murch explains what he sees as insurmountable problems with 3D movies:

The biggest problem with 3D, though, is the “convergence/focus” issue. A couple of the other issues — darkness and “smallness” — are at least theoretically solvable. But the deeper problem is that the audience must focus their eyes at the plane of the screen — say it is 80 feet away. This is constant no matter what.

But their eyes must converge at perhaps 10 feet away, then 60 feet, then 120 feet, and so on, depending on what the illusion is. So 3D films require us to focus at one distance and converge at another. And 600 million years of evolution has never presented this problem before. All living things with eyes have always focussed and converged at the same point.

That’s an interesting idea. It’s true the convergence and focus are two separate processes: when you look at something close to you, your eyes tilt in towards each other (convergence), and each eye shifts its focus. The latter process is known as accommodation and involves flexing muscles in the eye to change the power of the lens.

It’s certainly true that 3D movies involve one but not the other, and it’s possible in principle that this has an effect on how we perceive them, but I wouldn’t have thought it was a significant effect in practice. This is way outside of my expertise, but here’s how it seems to me anyway.

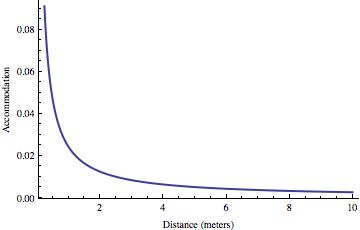
The eye is set up so that, when the muscles are completely relaxed, you’re focusing on points that are extremely far away — “at infinity”, as they usually say. The closer you want to focus, the more you have to strain the muscles. The amount of strain is very small for a wide range of distances, shooting up sharply as the distances get small. Here’s a graph I mocked up:

The horizontal axis is the distance to the object you’re looking at, and the vertical axis is the amount of strain the muscles have to provide — to be specific, it’s the fractional change in power of the lens, Delta f/f. In case you’re wondering, I assumed the diameter of the eye is 25 mm and the person’s near point is 25 cm. The graph starts at the near point, so the highest point on the graph is the maximum accommodation the person’s eye is capable of.

The point is that the things you’re looking at in a 3D movie are pretty much always “far away”, as far as accommodation is concerned. The range of examples Murch gives, from 10 feet (i.e. 3 meters) on up, is a good example.  Note that the graph is very flat for this range.

If 3D movies routinely involved closeups of a book someone was reading, or the construction of a ship in a bottle, that’d be different. But they don’t. Most of the time, the point you’re looking at is far enough away to be practically at infinity, so your visual system should be expecting not to have to do any accommodation. And of course it doesn’t have to, because the screen is really quite far away (essentially at infinity).

So it seems implausible to me that the accommodation / convergence problem really matters. But this is very, very far from any area of expertise of mine, so maybe I’m wrong.

The guys at Car Talk got a math-physics based puzzler wrong this week.  You can hear or read the question and their answer at their Web site.

The puzzler in question is labeled week of Jan. 17 as of now, but it should really be the week of Jan. 15 — in fact, the original question aired here in Richmond on the 14th. Anyway, it’s the one about how to tell when a cylindrical gas tank is 1/4 full.

Here’s what I wrote to them:

Sorry, but you got the answer to last week’s puzzler (i.e., the puzzler from Jan. 14, 2011) wrong. You assumed that the center of mass of an object has the property that there are equal amounts of mass on both sides, but that’s not true.

To convince yourself of this, think of the following example: take a 100-pound weight, and a 200-pound weight, and join them together with a long bar. The weight of the bar is small, say 1 pound. Now where’s the center of mass of this funny asymmetrical dumbbell? It’s somewhere between the two masses, about 2/3 of the way along the bar. But there’s certainly not the same amount of weight on the two sides of that point: there’s over 200 pounds on one side, and just over 100 pounds on the other.

In the case of a semicircle, the difference isn’t as dramatic as that, but there still is a difference. The center of mass is about 42.4% of the way out from the center (4/3pi, if you must know). The correct answer (i.e., the point where half the mass is on one side and half the mass is on the other) is only 40.3% of the way out.

Unfortunately, I don’t know a good way to answer the original question: I can’t think of a way to get the 40.3% value without some annoying calculus.

Update: Ray admits he got it wrong.

 I learned (from the Cosmic Variance blog) about a Web site with interesting discussions of a wide variety of questions in physics. It reminded me of some parts of my misspent youth.

Back in the 1990s, I spent a lot of time reading and posting articles on the various physics and astronomy Usenet newsgroups. For those who don’t know, newsgroups are forums in which people can discuss a huge variety of topics. They allowed freewheeling electronic communication back in the days before blogs, and even before the invention of the Web. Last time I checked, Usenet newsgroups still existed, but with all the other options out there nowadays, they don’t play the same role they used to.

Newsgroups had participants with a wide variety of backgrounds and interests. Participants in the physics newsgroups included graduate and undergraduate students, professional scientists, and tons and tons of interested laypeople. The freedom of anybody to participate was both a blessing and a curse. It made for a lot of variety, of course, but it also meant that discussions could easily be hijacked by crackpots. Some of the crackpots were highly entertaining, but eventually most serious people would get frustrated with all the noise and go away.

One solution to this problem was moderated newsgroups. I was one of the moderators of the group sci.physics.research for quite a while. One of us moderators would have to approve each post before it could appear in the newsgroup. The big problem with this, of course, was that it was labor-intensive.

OK, that’s it for the history lesson. What reminded me of all this is the Web site Physics Stack Exchange, which aims to produce a similar sort of forum for discussion of physics questions. The site has moderators, but they don’t approve each post manually as we did. Rather, the participants in the group vote answers up or down, so that the ones that are deemed most useful rise to the top. There’s a complicated set of rules whereby only people who have earned the right (through useful participation in the past) are allowed to vote.

Once I started looking at it, I couldn’t resist posting some answers of my own.

There’s a lot of good stuff there. Check it out, and participate if you’re interested!

Benjamin Bederson, physics professor emeritus at NYU, has a letter in today’s NY Times magazine:

As a physicist myself, I read with great interest Jonah Lehrer's article about Geoffrey West, who is interested in developing a general theory of cities from first principles. Physicists €” myself included €” are intrigued by the idea that application of rigorous laws in the world of natural science can inspire similar applications in other areas, including social ones.

It may be true that methods from the natural sciences can be fruitfully applied in the social sciences, but as a matter of diplomacy I’d rather physicists refrained from “we’re rigorous and you’re not” language.  Whether or not it’s true, I don’t think it’s helpful.

But that’s not what bothers me about this letter.  He goes on to say

This quest has been going on for a long time: for example, the efforts to apply the Heisenberg uncertainty principle to human behavior.

This would be fine, if he went on to clarify that “efforts to apply the Heisenberg uncertainty principle to human behavior” are utterly stupid and pointless.  In fact, he seems to think precisely the opposite, namely that such efforts are a good example of the use of natural-science ideas in the social sciences.

The Heisenberg uncertainty principle is often used as a metaphor, sometimes to convey the banal notion that it’s often hard to measure stuff, and sometimes to convey the slightly more interesting idea that measurements affect the system being measured.  I suppose that what Bederson means by “apply[ing] the Heisenberg uncertainty principle to human behavior” is simply that when you survey people the act of surveying them has an effect on them.  That’s true, but it’s much less interesting than the actual Heisenberg uncertainty principle.   It’s also such an obvious idea that it’s downright insulting to suggest that social scientists needed physicists’ help to figure it out.