Author: Ted Bunn

My old friend Allen Downey has a thoroughly sensible post about correlation and causation.

It is true that correlation doesn’t imply causation in the mathematical sense of “imply;” that is, finding a correlation between A and B does not prove that A causes B. However, it does provide evidence that A causes B. It also provides evidence that B causes A, and if there is a hypothetical C that might cause A and B, the correlation is evidence for that hypothesis, too.

If you don’t understand what he means by this, or if you don’t believe it, read the whole thing.

I do think he’s guilty of a bit of rhetorical excess when he says that “the usual mantra, ‘Correlation does not imply causation,’ is true only in a trivial sense.” I think that the mantra means something quite specific and valid, namely something like “correlation does not provide evidence for causation that’s as strong as you seem to think.” One often sees descriptions of measured correlations that imply that the correlation supports the hypothesis of causation to the exclusion of all others, and when that’s wrong it’s convenient to have a compact way of saying so.

But that’s a small quibble, which gets even smaller if I include the next phrase in that quote from Allen,

The point I was trying to make (and will elaborate here) is that the usual mantra, “Correlation does not imply causation,” is true only in a trivial sense, so we need to think about it more carefully [emphasis added].

I couldn’t agree more, and everything Allen goes on to say after this is 100% correct.

Sean Carroll has a post about a report by Laurence Yaffe on the state of funding for theoretical particle physics in the US, or more specifically in the Department of Energy, which historically has been the big funding source in this field. They both use the word “calamity” to describe the situation, but as far as I can tell the evidence cited doesn’t support that conclusion.

(For what it’s worth, I see that Peter Woit views the situation the same way I do. For some people, that will increase my credibility; for others it’ll decrease it.)

Yaffe’s abstract:

A summary is presented of data obtained from a grass-roots effort to understand the effects of the FY13 and FY14 comparative review cycles on the DOE-funded portion of the US high energy theory community and, in particular, on graduate students and postdoctoral researchers who are beginning their careers. For a sample comprised of nearly all of the larger groups undergoing comparative review, total funding declined by an average of 23%, with numerous major groups receiving reductions in the 30–55% range. Funding available for postdoc or graduate student support declined over 30%, with many reductions in the 40–65% range. The total number of postdoc positions in this large sample of theory groups is declining by over 40%. The impacts on young researchers raise grave concerns regarding continued U.S. leadership in high energy theory.

Carroll:

Obviously this is unsustainable, unless as a society we make the decision that particle physics just isn’t worth doing. But hopefully things can be rectified at least a bit, to restore some of that money.

But the striking thing about Yaffe’s report is that it says precisely nothing about the total level of DOE funding in this field. What it says instead is that existing large particle theory research groups have had their funding cut. Is that because the funding is going away or because it’s going to other, smaller groups? As far as I can tell, Yaffe and Carroll assume the former, but they provide no evidence for it.

DOE did recently change their procedure for evaluating grants in various ways. According to Yaffe,

Three years ago, the Office of High Energy Physics (OHEP) within the Department of Energy made significant changes in how university-based research proposals are reviewed, switching to a comparative review process and synchronizing all new grants. Overt goals included decreasing the effects of historical inertia on funding levels for different groups, ensuring a level playing field, and moving to a start date for grants mid-way through the federal fiscal year by which time, it was hoped, Congressional funding decisions would normally be known.

The first two of those goals, it seems to me, pretty much say that the DOE is aiming to redistribute funds away from previously-large research groups (those that have benefitted from “historical inertia”). Yaffe gathered data on large research groups and showed they got smaller, precisely as you’d expect. So it’s not at all clear to me that the alarmist response to this information is warranted.

What we really need to know is simply how much funding high energy theory is getting in comparison with past years. That information isn’t as easy to find as you might think. The most recent DOE budget request does show a drop in high energy theory funding, but a more modest one than Yaffe’s figures, and in any case that wouldn’t have shown up in the figures yet. Over the few previous years, things seem pretty stable. Of course, “stable” in nominal terms is a modest de facto decline in real terms, but nothing like the proclaimed “calamity.”

I’m not a particle theorist, and I don’t deal with DOE, so I haven’t paid close attention to DOE funding levels over the years. It’s certainly possible that I’m missing something here. If anyone knows what it is, I’d be interested to hear.

Notes:

1. One can take the view that the government has no business funding pure curiosity-driven research like particle theory anyway. I don’t agree with that view, although I do understand it.
2. One can take the more moderate view that, even if the government should be funding things like particle theory, previous funding levels were too high and so a cut isn’t a “calamity.” I don’t have that great a sense of what funding levels are like in particle theory, so it’s hard for me to say for sure what I think about that. In general, I think we should be funding more science, not less, but then as a (modest) beneficiary of government research grants, I would think that, wouldn’t I?

Nature has a depressing piece about how to interpret p-values (i.e., the numbers people generally use to describe “statistical significance”). What’s depressing about it? Sentences like this:

Most scientists would look at his original P value of 0.01 and say that there was just a 1% chance of his result being a false alarm.

If it’s really true that “most scientists” think this, then we’re in deep trouble.

Anyway, the article goes on to give a good explanation of why this is wrong:

But they would be wrong. The P value cannot say this: all it can do is summarize the data assuming a specific null hypothesis. It cannot work backwards and make statements about the underlying reality. That requires another piece of information: the odds that a real effect was there in the first place. To ignore this would be like waking up with a headache and concluding that you have a rare brain tumour — possible, but so unlikely that it requires a lot more evidence to supersede an everyday explanation such as an allergic reaction. The more implausible the hypothesis — telepathy, aliens, homeopathy — the greater the chance that an exciting finding is a false alarm, no matter what the P value is.

The main point here is the standard workhorse idea of Bayesian statistics: the experimental evidence gives you a recipe for updating your prior beliefs about the probability that any given statement about the world is true. The evidence alone does not tell you the probability that a hypothesis is true. It cannot do so without folding in a prior.

To rehash the old, standard example, suppose that you take a test to see if you have kuru. The test gives the right answer 99% of the time. You test positive. That test “rules out” the null hypothesis that you’re disease-free with a p-value of 1%. But that doesn’t mean there’s a 99% chance you have the disease. The reason is that the prior probability that you have kuru is very low. Say one person in 100,000 has the disease. When you test 100,000 people, you’ll get  roughly one true positive and 1000 false positives. Your positive test is overwhelmingly likely to be one of the false ones, low p-value notwithstanding.

For some reason, people regard “Bayesian statistics” as something controversial and heterodox. Maybe they wouldn’t think so if it were simply called “correct reasoning,” which is all it is.

You don’t have to think of yourself as “a Bayesian” to interpret p-values in the correct way. Standard statistics textbooks all state clearly that a p-value is not the probability that a hypothesis is true, but rather the probability that, if the null hypothesis is true, a result as extreme as the one actually found would occur.

Here’s a convenient Venn diagram to help you remember this:

(Confession: this picture is a rerun.)

If Nature‘s readers really don’t know this, then something’s seriously wrong with the way we train scientists.

Anyway, there’s a bunch of good stuff in this article:

The irony is that when UK statistician Ronald Fisher introduced the P value in the 1920s, he did not mean it to be a definitive test. He intended it simply as an informal way to judge whether evidence was significant in the old-fashioned sense: worthy of a second look.

Fisher’s got this exactly right. The standard in many fields for “statistical significance” is a p-value of 0.05. Unless you set the value far, far lower than that, a very large number of “significant” results are going to be false. That doesn’t necessarily mean that you shouldn’t use p-values. It just means that you should regard them (particularly with this easy-to-cross 0.05 threshold) as ways to decide which hypotheses to investigate further.

Another really important point:

Perhaps the worst fallacy is the kind of self-deception for which psychologist Uri Simonsohn of the University of Pennsylvania and his colleagues have popularized the term P-hacking; it is also known as data-dredging, snooping, fishing, significance-chasing and double-dipping. “P-hacking,” says Simonsohn, “is trying multiple things until you get the desired result” — even unconsciously.

I didn’t know the term P-hacking, although I’d heard some of the others. Anyway, it’s a sure-fire way to generate significant-looking but utterly false results, and it’s unfortunately not at all unusual.

Some issues of grammar and usage come up fairly regularly in students’ writing. These are a few I’ve noticed in past semesters. I’ll illustrate them with (anonymous) excerpts from past student essays.

This is definitely not meant to be a complete list. It’s just issues that have struck me particularly often.

The comma splice.

This is by far the most common grammar or punctuation error in my students’ writing.

A comma splice is the joining together of two complete clauses by just a comma. For example,

Ptolemy has made it so Earth is not in the exact center of his model, it is displaced slightly.

The part before the comma is a grammatically complete sentence, and so is the second part. Joining them together with just a comma is an error.

There are several ways to fix a comma splice:

• Just make the two halves separate sentences.
• If you want to emphasize that they’re closely related, you can separate them by a semicolon (;) or maybe a colon (:). The semicolon is more common; the colon usually suggests that the second half explains or provides an example of whatever’s in the first half.
• Put a conjunction (and, but, etc.) in between the two clauses.

There’s an important addendum to the last rule: “however” is not a conjunction, so it doesn’t fix a comma splice. For example:

All the above theories are strong candidates for the explanation of how we observe the heavens, however, only one of them soundly holds the upper-hand beyond the other two and that is the Tychonic model.

This contains a comma splice error. Replacing the comma after “heavens” with a semicolon solves the problem. (The comma after “however” is correct and necessary.)

The subjunctive.

There was a popular song in the 1990s called “What if God was one of us?” This song drove grammar nerds crazy, because it should be “What if God were one of us?” The old musical Fiddler on the Roof got this right, in the name of the song “If I were a rich man.”

The quick-and-dirty rule is this: if you write an “if” clause, and the thing in that clause is something known to be false, then use “were” instead of “was”. In this situation, “were” is the subjunctive form of “was”.

For example:

If the earth was really rotating once a day, we would have been hurled into the universe by now because of the speed.

Change “was” to “were” in this sentence.

(In hindsight, this is a poor example, because the Earth actually does rotate once per day! But this essay was written from the point of view of an anti-Copernican, who believed it was false.)

Beg the question.

An example of how this expression is often used:

This begs the question, can a theory be considered correct if it simply cannot be proven wrong?

The meaning here is clear: “begs the question” is being used to mean something like “raises the question” or “requires us to examine the question.”

The problem is that, traditionally, “beg the question” meant something quite different. It referred to a particular form of logical error, in which a person making an argument assumed the very thing he or she was trying to prove. In other words, accusing someone of “begging the question” means accusing them of circular reasoning.

Idiomatic expressions change over time. Nowadays, the original meaning of “beg the question” is quite uncommon. The phrase is much more commonly used in the sense that the student above meant. But at the moment, traditionalists regard the more modern meaning as “incorrect.”

You might think the traditionalists are being stupid to insist on an archaic meaning. You might say that since everybody instantly understands the intended meaning, there’s no problem. Between you and me, I might even agree with you. But some significant fraction of your readers, particularly if you’re writing papers for college professors, will insist that the newer meaning of this expression is “wrong” and will judge you negatively for it.

This puts “beg the question” in a strange position. If you use it in the old-fashioned, correct sense, lots of people won’t understand you. If you use it in the more current sense, traditionalists will sneer at you. There’s only one solution: avoid the phrase entirely. Fortunately, this isn’t hard to do. Often “raises the question” conveys the meaning you want.

As Bryan Garner put it in his very good book A Dictionary of Modern American Usage,

When a word undergoes a marked change from one use to another . . . it’s likely to be the subject of dispute. Some people (Group 1) insist on the traditional use; others (Group 2) embrace the new use. . . . Any use of [the word] is likely to distract some readers. The new use seems illiterate to Group 1; the old use seems odd to Group 2. The word has become “skunked.”

Beginning a sentence with “So.”

An example:

So when reflecting upon the theories of the best astronomical minds of this era, one cannot help but be swayed by the system that takes the best of each theory.

This is more a matter of taste than of correctness, but I recommend that you not start sentences with “So” in formal writing. Traditionally, “so” is a conjunction, so it should join two clauses together (as it just did in this sentence). I won’t say that using it as an adverb to start a sentence is wrong, but it sounds chatty and informal to me. If you’re going for a traditional, formal tone in your writing, I recommend avoiding it. If you’re deliberately trying to sound conversational, that’s a different matter.

In general, use the word “that” even when it’s optional.

Compare these two sentences:

• If the Earth were in motion as Copernicus claims, the Bible would read the Earth stood still.
• If the Earth were in motion as Copernicus claims, the Bible would read that the Earth stood still.

Both are 100% grammatically correct, but the second one’s better, for a subtle reason. In the first sentence, when you get to the words “read the Earth,” you have a momentary tendency to misinterpret it: it looks, just for an instant, as if “Earth” were a direct object. That is, you briefly interpret “read the Earth” in the same way as you would interpret “read the book.” When you get to the rest of the sentence, the confusion is cleared up, but that slight hiccup disrupts your attention just a bit. By including the word “that,” even though it’s not grammatically necessary, the author keeps the hiccup from happening.

This advice goes against one of the most common writing maxims, namely to be concise and omit needless words. But I still think you’re usually better off including “that” in situations like this. The best thing to do is to read the sentence aloud both ways and decide which one sounds better.

Let me repeat that this is not a matter of correctness: both versions of the sentence above is correct. All I ask you to do is consider whether one version or the other is better at helping the reader understand what you mean.

The passive voice.

Lots of people will tell you to avoid writing sentences in the passive voice. For instance, instead of saying

The issue of whether light travels instantaneously or at a finite speed has been debated by many great minds.

say

Many great minds have debated the issue of whether light travels instantaneously or at a finite speed.

For those who don’t remember their grammar terminology, in an active sentence, the subject of the sentence is the person or thing performing the action in the sentence. In the above examples, the action is debating, and the things doing the debating are the minds. The second version puts the actor right up front as the subject of the sentence. That’s active, and the conventional wisdom is that active is better.

Personally, I think that the blanket rule to avoid the passive is often overstated. (I rambled on about this at some length in another post.) There are lots of times when the passive voice is just what you want. But without a doubt there are many cases, including the above sentence, in which the passive voice sounds bad. My advice: whenever you write a passive sentence, try out what it sounds like if you make it active. Read both versions aloud, and see which one sounds better. More often than not, you’ll decide to make it active.

I’m teaching a cosmology course at the moment, in which we talk a lot about curved space. As usual in this sort of situation, I’m trying to make my students build up some intuition about what life is like on curved two-dimensional surfaces, which are easier to grasp than curved three-dimensional space. In that spirit, I asked them a question from our textbook (Ryden’s Introduction to Cosmology), which can be paraphrased

What is the area of the largest equilateral triangle you can draw on a sphere of radius R?

The ground rules here is that a triangle is bounded by “straight lines” on the surface of the sphere. A straight line (formally called a geodesic) on a curved surface is a curve that gives the shortest distance between two points (as long as those points aren’t too far apart). On a sphere, the straight lines are great circles (circles whose center is the center of the sphere).

For instance, here’s a triangle each of whose sides is a quarter of a great circle:

It has the funny property that all of its angles are right angles.

You can go bigger than this, though. Here’s a little animation showing equilateral triangles of different sizes:

The biggest one is one with three 180-degree angles, covering half the sphere. You take a single great circle (“straight line”), mark off three equally spaced point, and call those the vertices.

At least, that’s what I intended the answer to be (and I’m pretty sure it’s what the textbook author intended too). But a student in the class argued for a different answer. Ultimately, the difference between his answer and mine is a matter of definition, so you can say that either is “right,” but I have to confess that I like his answer better than mine.

I’ll show you his answer below.

Continue reading Spherical triangles

People have been asking me about Stephen Hawking’s recent statement about black holes, under the mistaken impression that I know a lot about it. In case you missed it, here’s Nature’s take, and here’s Hawking’s actual preprint.

I think I know enough to say what the main idea is, although I certainly don’t know enough to evaluate the merits of Hawking’s proposal. I actually think that the whole business is more interesting for what it has to say about the process of communicating science anyway, so I’ll try to summarize the idea and then make some broader comments. If you skip ahead to the end, I won’t be terribly offended. I promise to say mean things about Hawking there, so don’t miss it.

There’s a fairly longstanding puzzle about what happens when you try to apply quantum mechanics to black holes. As Hawking argued long ago, quantum effects should cause black holes to emit radiation and gradually dwindle away. Later, people realized that this led to a problem. The predicted Hawking radiation was essentially random (thermal). As a result, almost all information about the material that went into forming the black hole was lost. You could form a black hole by throwing together all the books in the Library of Congress (along with a bunch of other stuff), and by the time it all radiated away there’d be no “memory” of any of that information.

This is a problem because there are broad principles in quantum physics that say that information is not lost. If you know the complete quantum state of a system at one time, you should be able to work out its complete quantum state (all the information it contains) at any other time, either earlier or later. The randomness of Hawking radiation is inconsistent with that. We don’t yet know the correct theory of quantum gravity, but if information is lost in black holes, it implies that that theory, whatever it might be, is inconsistent with what seem at the moment to be very fundamental principles.

In a more recent development, which I definitely don’t understand, some people have proposed that you can resolve this paradox by saying that there’s a “firewall” of intense radiation right at the horizon of any black hole.

What Hawking suggests in his recent preprint is that the paradox can be resolved by suggesting that black holes don’t actually have an event horizon but merely an apparent horizon. This raises some obvious questions: What the heck are these two types of horizon? Why does it matter what kind a black hole has? I’m not sure I know the answer to the second one, but I can tell you about the first one.

Let’s start with event horizons. By definition, an event horizon is the boundary of the causal past of future null infinity. That makes everything perfectly clear, right?

No? OK. Here’s a translation. If you’re inside of an event horizon, then neither you nor any signal you send out (traveling at speeds up to and including the speed of light) can escape and get out to arbitrarily great distances. If I’m outside the horizon, and you’re inside, then there’s no way you can get information to me.

An apparent horizon surrounds a region of space called a trapped region. In a trapped region, you can fire off a light signal directly away from the center, but it still moves toward the center. (I’m being slightly imprecise here, but not in a way that does any serious damage, I think.)

Those two concepts sound very similar, and indeed they are, but they’re not identical. The definition of an event horizon has to do with what happens to the signals you send out in the arbitrarily far future, whereas an apparent horizon is defined by what the signals do right away. You can in principle imagine a situation in which you send out light signals, and they all start heading in toward the center of the black hole, but later something changes and some of them manage to make it out. Then you’re inside an apparent horizon but not an event horizon. (There’s a theorem due to Hawking that says that this can’t happen under normal circumstances, but that theorem is based on classical physics, not quantum physics, so we can’t use it here.)

Here’s a diagram that may (or may not!) help.

This diagram, which I stole from an excellent blog post by  an actual expert, shows an evaporating black hole. Here are the rules for interpreting it.

1. Time increases as you go up.
2. Signals that travel at the speed of light go at 45 degrees. Anything slower than that moves up the diagram along a steeper path.
3. If you hit r = 0, you “reflect off” and go back the way you came.
4. Distances are grossly distorted. In fact, the two diagonal lines labeled with those funny script-J characters are actually infinitely far away.

In this diagram, the diagonal line directly above the letters “R(t)” is the event horizon. Note that, if you’re above that line, in the little right-triangle region, any light signal you send out is guaranteed to hit the singularity, rather than making to the outside.

Here’s another diagram, stolen from an article by Hossenfelder and Smolin, illustrating another possibility.

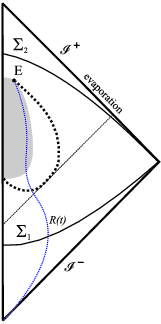
This picture shows a what a black hole might look like without an event horizon. The shaded gray region is the area where weird quantum effects are important, so we don’t know what’s going on. The thick dotted line is an apparent horizon: if you’re inside there, then every light signal you send starts going in toward the horizon. (That’s not obvious from the picture, but take my word for it.) But there is no singularity, so those light signals eventually pass close to the center and then make it back out.

To phrase things in a way that will give fits to the actual experts (in the unlikely event that any have read this far), in this scenario light signals start to be pulled in toward the black hole, but the black hole evaporates out from under them before they hit a singularity, and so they subsequently make it out.

Hawking’s proposal is that black holes are like the second diagram, not the first one.

Now why does this matter? Well, I gather that the information-destroying property of black holes has to do with the existence of an actual event horizon. If light signals literally never make it out, then information is lost. If they just take a long time to get out, as in the case of an apparent horizon, then the information is in principle preserved, and there’s no problem. At least that’s what I understand Hawking to be saying, although whether he’s right or not I can’t say.

OK. On to some

Broader Remarks

First, neither Hawking nor anyone else is claiming that this makes any difference to what we see in practice. The actual black holes we see are so large that their evaporation is completely negligible. Our understanding of their behavior is unchanged by any of this. The question here is a sort of abstruse one: does the information that falls into a black hole disappear in a singularity, or does it “survive” until the end stages of black hole evaporation and then sneak out? This may make a big difference in our understanding of theoretical physics, but it doesn’t change the behavior of anything under “normal” circumstances.

Because of this, some people have complained bitterly about news reports breathlessly announcing things like “Hawking claims that black holes don’t exist.” It’s true that those headlines suggest something much more dramatic than Hawking’s actual claim, which is unfortunate. But in this instance I have to absolve the poor headline-writers of most of the blame. After all, here’s a direct quote from Hawking’s article:

The absence of event horizons mean that there are no black holes – in the sense of regimes from which light can’t escape to infinity. There are however apparent horizons which persist for a period of time. This suggests that black holes should be redefined as metastable bound states of the gravitational field.

If Hawking didn’t want people to jump to that conclusion, he shouldn’t have said this in this way.

But it seems to me that Hawking is guilty of something far worse. If you read the actual article, you’ll find no hint that anyone has suggested anything like this before.  I’m not an expert in this field, but as far as I can tell this is decidedly not the case. For instance, the Hossenfelder-Smolin paper that I stole that diagram from lays out this possibility quite clearly and cites a number of previous works that apparently discuss similar ideas. None of these works are mentioned.

I’d be interested to know what actual researchers in this field think, but I find it hard to see any way to escape the conclusion that this is an appalling failure to uphold basic academic standards.

(Note: Hawking’s article is a summary of a talk he gave and is not apparently submitted for publication in a journal. I don’t think that provides any sort of excuse, but maybe others do.)

I didn’t think much of Steven Pinker’s New Republic essay on “scientism” (i.e., the tired old science-vs-humanities squabble), but it did initiate an stream of amusingly stupid responses.

First came Leon Wieseltier’s response, also in the New Republic, which was a stellar example of missing the point. Although he claims to be arguing against Pinker, he spends most of his time railing against a position that Pinker very explicitly disavows (namely that scientific understanding is the only kind of understanding worth having, or that the sciences can and should subsume the humanities). By far the most interesting question raised by Wieseltier’s piece is the question of whether Wieseltier can’t understand what he reads or is deliberately misrepresenting Pinker.

Wieseltier also wins stupidity points for repeatedly using the absurd word “scientizer.”

But by far the most amusingly silly response is Daniel Dennett’s defense of Pinker. Dennett  thinks that Wieseltier’s arguments are too silly to deserve attention, so he devotes himself to sarcasm. I have to admit that I liked this line,

Pomposity can be amusing, but pomposity sitting like an oversized hat on top of fear is hilarious.

but (a) this sort of thing is clearly of precisely no value in convincing anyone of anything they don’t already believe, and (b) when it comes to pomposity (although perhaps not fear), Dennett’s at least a bit vulnerable to a pot-kettle problem.

There’s just one thing in this whole business that I think is actually a bit interesting. On the subject of science vs. religion, Wieseltier says

Pinker tiresomely rehearses the familiar triumphalism of science over religion: “the findings of science entail that the belief systems of all the world’s traditional religions and cultures … are factually mistaken.” So they are, there on the page; but most of the belief systems of all the world’s traditional religions and cultures have evolved in their factual understandings by means of intellectually responsible exegesis that takes the progress of science into account; and most of the belief systems of all the world’s traditional religions and cultures are not primarily traditions of fact but traditions of value; and the relationship of fact to value in those traditions is complicated enough to enable the values often to survive the facts, as they do also in Aeschylus and Plato and Ovid and Dante and Montaigne and Shakespeare.

Wieseltier has one valid and important point here. The more strident anti-religion types love to argue as if all religious people were knuckle-dragging fundamentalists who think the Earth is 6000 years old. This is simply not the case, and by pretending it is such people are attacking a straw man. But Wiesltier himself shades the truth in the opposite direction when he says

Most of the belief systems of all the world’s traditional religions and cultures are not primarily traditions of fact but traditions of value

I’m no expert on the sociology of religion, but I’m confident that this statement is not true, at least not in any sense that’s useful for thinking about the relationship between science and religion in contemporary America.

As Wieseltier is no doubt aware, there are lots and lots of people in the world for whom statements of fact, such as “A particular man was born of a virgin, died, and later rose from the dead” are extremely important parts of their religious tradition. Following Stephen Jay Gould’s infamous idea of non-overlapping magisteria, Wieseltier simply defines religious tradition in a way that does not include such people.

There are indeed many religious people for whom questions of value and meaning, rather than questions of fact, are the only things that matter about their religion. I know quite a few of them, and I wouldn’t be surprised if the vast majority of the religious people in Wieseltier’s social circle are in this category. But there are many people — at a guess, and without any data, I’d say far more people, in the US at any rate –for whom this isn’t true. For every Christian who says that it’s not important whether the Resurrection actually happened (I know of at least one Episcopal priest who says this), I bet there are a whole bunch who say that anyone who thinks that way isn’t really a Christian.

I can understand the intellectual appeal of defining the problems of science and religion out of existence, but if you’re interested in understanding how the two cultures actually interact in present-day society, this solution won’t do.

I like to brag about my students, so let me point out that, when you search YouTube for “parallax,” the number one hit is a video made by UR student Eric Loucks as a part of my first-year seminar course, Space is Big.

Great job, Eric!

Scientific American has an article about 7 Misused Science Words. Number 2 is “theory”:

Part of the problem is that the word “theory” means something very different in lay language than it does in science: A scientific theory is an explanation of some aspect of the natural world that has been substantiated through repeated experiments or testing. But to the average Jane or Joe, a theory is just an idea that lives in someone’s head, rather than an explanation rooted in experiment and testing.

Although of course I applaud the broader point they’re making — saying something is “just a theory,” as, e.g., anti-evolution types do, isn’t an argument against its validity — this doesn’t sound right to me. A theory may have been experimentally substantiated, but it need not have been.

Is string theory (which is notoriously untested by experiment) not a theory? Was general relativity not a theory during the several decades during which it had minimal experimental support?

The article supports this definition with a link to a post at something called Livescience, which says (in its entirety)

A scientific theory summarizes a hypothesis or group of hypotheses that have been supported with repeated testing. If enough evidence accumulates to support a hypothesis, it moves to the next step—known as a theory—in the scientific method and becomes accepted as a valid explanation of a phenomenon.

In my experience, this is not how scientists use the word. I know lots of physicists who come up with theories willy-nilly, and don’t feel the need to wait for experimental evidence before labeling them “theories.”

In the unlikely event that any creationists read this, let me reiterate: I am not saying that a theory necessarily lacks experimental support, so saying something is “just a theory” doesn’t constitute a logical argument against it. In particular, Darwinian evolution is a theory, which happens to be buttressed by phenomenal amounts of evidence.

Granted, this is pretty much just a quibble. I’m just easily irritated by cartoon descriptions of “the scientific method,” formed without paying much attention to what scientists actually do and then glibly repeated by scientists.

Mother Jones has a writeup of a very interesting psychology study on how political views affect people’s ability to draw mathematical conclusions.

A group of psychologists gave a bunch of people a math problem:

Lots of people get this wrong. (That’s not the surprising part.)

Here’s where things get more interesting. They changed the problem into one about gun control: leaving the numbers exactly the same, they posed the problem as one about whether cities that enact gun control laws saw an increase or a decrease in crime. They also surveyed the participants to determine (a) their political views and (b) some sort of measure of their numeracy. In both the skin-rash and gun-control cases, they had two versions of the question, in which all that was switched was the right answer — that is, they interchanged the labels “Rash got better” and “Rash got worse,” leaving all the numbers unchanged.

The results:

The top graph is for the skin-rash version of the study. The bottom rash is the gun-control version. In time-honored fashion, red is conservative and blue is liberal.

No big surprises in the skin-rash results (except possibly the suggestion that the curves rise a bit at very low numeracy, but I don’t know how significant that is). The action is all in the lower graph, which indicates the following:

1. Both liberals and conservatives are more likely to get the answer right when it accords with their political preconceptions.
2. For liberals, there’s a large difference only among the highly numerate — the innumerate do equally badly whichever political valence they see.

Fact 1 is interesting but not astonishing. Fact 2 is the really fascinating one.

The proposed explanation:

Our first instinct, in all versions of the study, is to leap instinctively to the wrong conclusion. If you just compare which number is bigger in the first column, for instance, you’ll be quickly led astray. But more numerate people, when they sense an apparently wrong answer that offends their political sensibilities, are both motivated and equipped to dig deeper, think harder, and even start performing some calculations—which in this case would have led to a more accurate response.

“If the wrong answer is contrary to their ideological positions, we hypothesize that that is going to create the incentive to scrutinize that information and figure out another way to understand it,” says Kahan. In other words, more numerate people perform better when identifying study results that support their views—but may have a big blind spot when it comes to identifying results that undermine those views.

What’s happening when highly numerate liberals and conservatives actually get it wrong? Either they’re intuiting an incorrect answer that is politically convenient and feels right to them, leading them to inquire no further—or else they’re stopping to calculate the correct answer, but then refusing to accept it and coming up with some elaborate reason why 1 + 1 doesn’t equal 2 in this particular instance. (Kahan suspects it’s mostly the former, rather than the latter.)

The Mother Jones article suggests that “both liberals and conservatives” show effect number 2 — highly numerate people being more biased than less numerate people — but from the graph the effect seems much smaller for the conservatives. It seems to me that the liberals are the ones whose behavior needs explaining.

With that caveat, this explanation may well be right, but I wonder if there might be other effects. Maybe highly numerate liberals differ from less numerate liberals in some other way, such as more strongly-held political views. I’m not necessarily espousing that speicfic explanation; I’m just wondering. I’d be interested to hear other ideas.