I’m teaching a cosmology course at the moment, in which we talk a lot about curved space. As usual in this sort of situation, I’m trying to make my students build up some intuition about what life is like on curved two-dimensional surfaces, which are easier to grasp than curved three-dimensional space. In that spirit, I asked them a question from our textbook (Ryden’s Introduction to Cosmology), which can be paraphrased
What is the area of the largest equilateral triangle you can draw on a sphere of radius R?
The ground rules here is that a triangle is bounded by “straight lines” on the surface of the sphere. A straight line (formally called a geodesic) on a curved surface is a curve that gives the shortest distance between two points (as long as those points aren’t too far apart). On a sphere, the straight lines are great circles (circles whose center is the center of the sphere).
For instance, here’s a triangle each of whose sides is a quarter of a great circle:
You can go bigger than this, though. Here’s a little animation showing equilateral triangles of different sizes:
The biggest one is one with three 180-degree angles, covering half the sphere. You take a single great circle (“straight line”), mark off three equally spaced point, and call those the vertices.
At least, that’s what I intended the answer to be (and I’m pretty sure it’s what the textbook author intended too). But a student in the class argued for a different answer. Ultimately, the difference between his answer and mine is a matter of definition, so you can say that either is “right,” but I have to confess that I like his answer better than mine.
I’ll show you his answer below.
Here’s my student’s observation. Consider a picture like this:
We naturally think of the red region as the triangle, but isn’t the blue region a triangle too? After all, it’s a region of the surface completely surrounded by three straight line segments. We can shrink the red triangle as small as we want and make the blue triangle as close as we want to the entire sphere. So the answer is that there are equilateral triangles with any area up to (but, I guess, not including), the surface area of the entire sphere.
The point is that, when you draw a closed curve on a sphere, there’s not necessarily a natural, principled distinction between the “inside” and the “outside” the way there is on an infinite plane.
You could, if you like, define a triangle to be the smaller of the two regions delimited by three line segments — that’s what I mean when I say that the difference between the two answers is a matter of definition. But I have to say that that definition is pretty unnatural. For one thing, what do you do when the two regions are equal in area? Also, that definition has the ugly property that you can move one vertex of a triangle a small amount and have the “inside” and “outside” flip in a discontinuous manner (if the triangle is close to half the sphere in size). So I think that my student’s answer is better than mine.
I always like when that happens.
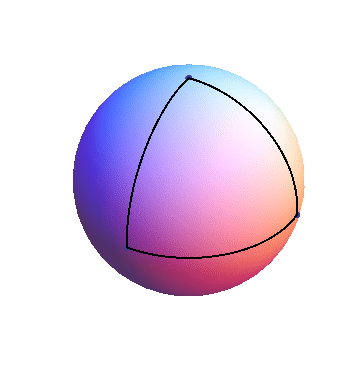

What I love about this question is that it gets students thinking about the definition of a triangle…