Knowing my interest in such things, my brother Andy pointed me toward an article in Science by Bradly Efron on Bayesian and frequentist statistical techniques. I think it’s behind a paywall, unfortunately.
Efron is obviously far more qualified to discuss this than I am — he’s a professor of statistics at Stanford, and I’ve never taken a single course in statistics. But, with the physicist’s trademark arrogance, I won’t let that stop me. As far as I can tell, much of what he says is muddled and incoherent.
Near the beginning, Efron gives a perfectly serviceable example of Bayesian inference:
A physicist couple I know learned, from sonograms, that they were due to be parents of twin boys. They wondered what the probability was that their twins would be identical rather than fraternal. There are two pieces of relevant evidence. One-third of twins are identical; on the other hand, identical twins are twice as likely to yield twin boy sonograms, because they are always same-sex, whereas the likelihood of fraternal twins being same-sex is 50:50. Putting this together, Bayes’ rule correctly concludes that the two pieces balance out, and that the odds of the twins being identical are even.
So far so good. Then, a couple of paragraphs later:
Bayes’ 1763 paper was an impeccable exercise in probability theory. The trouble and the subsequent busts came from overenthusiastic application of the theorem in the absence of genuine prior information, with Pierre-Simon Laplace as a prime violator. Suppose that in the twins example we lacked the prior knowledge that one-third of twins are identical. Laplace would have assumed a uniform distribution between zero and one for the unknown prior probability of identical twins, yielding 2/3 rather than 1/2 as the answer to the physicists’ question. In modern parlance, Laplace would be trying to assign an “uninformative prior” or “objective prior”, one having only neutral effects on the output of Bayes’ rule. Whether or not this can be done legitimately has fueled the 250-year controversy.
I have no idea whether Efron’s description of what Laplace would have thought is correct (and, I suspect, neither does Efron). But assuming it is, is the reasoning correct? Everybody agrees that, given the assumed prior, Bayes’s rule gives the correct recipe for calculating the final probability. The question is whether imaginary-Laplace used the right prior.
That question is, unfortunately, unanswerable without mind-reading. The correct prior for imaginary-Laplace to use is, unsurprisingly, the one that accurately reflected his prior beliefs. If imaginary-Laplace believed, before looking at the sonogram, that all possible values for the probability were equally likely — that is, if he would have been equally unsurprised by a divine revelation of the true value, whatever value was revealed — then the result is correct. If, on the other hand, he believed, based on his prior life experience, that some values of the probability were more likely than others — say, he’d encountered a lot more fraternal than identical twins in his life — then he would have been wrong to use a uniform prior.
The conclusion imaginary-Laplace comes to depends on what he thought before. Many people who dislike Bayesian statistics state that fact as if it were a problem, but it’s not. New evidence allows you to update your previous beliefs. Unless that evidence tells you things with logical certainty, that’s all it does. If you expect more than that, you’re asking your data to do something it just can’t do.
Efron claims that the traditional, non-Bayesian approach to statistics, known as “frequentism,” has the advantage that it “does away with prior distributions entirely,” with a resulting “gain in scientific objectivity.” This is true, I guess, but at a cost: Frequentism simply refuses to answer questions about the probability of hypotheses. To be specific, suppose that you went back to those expectant physicists and told them that they were only allowed to use frequentist reasoning and could not take into account their prior knowledge. You then asked them, based on the sonogram results, about the probability that their twins were identical. Frequentism flatly refuses to answer this question.
What this means in practice is that frequentism refuses to answer any actually interesting questions. Want to know whether the physicists at the LHC have found the Higgs boson? Don’t ask a frequentist. If he’s honest, he’ll admit that his methods can’t answer that question. All a frequentist can tell you is the probability that, if the Higgs boson has a certain set of properties, then the LHC folks would have gotten the data they did. What’s the probability that the Higgs actually has those properties? A frequentist can’t say.
For those who care, let me state that precisely. In frequentist analyses, all probabilities are of the form P(data | hypothesis), pronounced “the probability that the data would occur, given the hypothesis.” Frequentism flatly refuses to consider probabilities with the hypothesis to the left of the bar — that is, it refuses to consider the probability that any scientific hypothesis is correct.
The situation can be summarized in a Venn diagram:
One might naively have supposed that this would generally be regarded as a problem.
This makes the advice with which Efron concludes his article particularly silly: in the absence of strong prior information, he says,
Bayesian calculations cannot be uncritically accepted and should be checked by other methods, which usually means frequentistically.
This is meaningless. The Bayesian questions that depend on the prior are precisely those that frequentism refuses to address. If you don’t like Bayesian methods, your only choice is to decide that you’re not interested in the questions those methods answer. It’s a mystery to me how scientists make themselves go to work in the morning while believing that it’s impossible for their data to tell them anything about scientific hypotheses, but apparently many do.
(Actually, I’m pretty sure I do know how they do it: even the frequentist scientists are actually closet Bayesians. They cheerfully use the data to update their mental tally of how likely various hypotheses about the world are to be true, based on their prior beliefs.)
In the last part of the article, Efron advocates for an approach he seems to have developed called “Empirical Bayes.” I find the details confusing, but the claim is that, in some situations involving large data sets, “we can effectively estimate the relevant prior from the data itself.” As a matter of logic, this is of course nonsense. By definition, the prior is stuff you thought before you looked at the data. I think that what he means is that, in some situations involving large data sets, the evidence from the data is very sharply peaked, so that the conclusions you draw don’t depend much at all on the prior. That’s certainly true in some circumstances (and has been well known to all practitioners of Bayesian statistics forever).
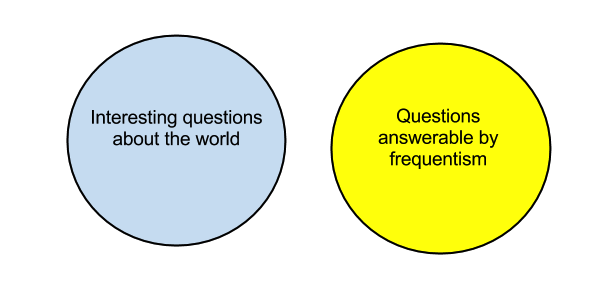
Ted, you’re a star. Please may I am copy your Venn diagram and put it up in my office – and use it in teaching!
Of course!
Amen! The frequentist folks would do well to read some Jaynes…
Great post.
Ian, Jaynes is absolutely the last thing the frequentist folks should read because he argues for a unique uninformative prior, which is exactly the sort of thing that caught out fictional Laplace in the above article. What everyone interested in this should read is Howson and Urbach http://www.amazon.com/books/dp/0812692357 If that does not cure you of the frequentist disease then nothing will.
Agreed. Jaynes was a strong advocate but he did get a lot of stuff wrong. Can’t vouch for Howson and Urbach, but there are a lot of good books around these days. There’s nobody I agree with 100% though 🙂
I have not read Efron’s piece, sorry! But maybe you can assess for me, in his “empirical Bayes” thinking, is it possible he is just taking steps towards hierarchical inference? Nice article, thanks – Ill be giving it to students to think about!
Phil — I don’t know exactly what hierarchical inference is, and I don’t understand exactly what Efron’s getting at in this part of his article, so I think I won’t offer a guess about whether they’re connected.
I will say that I’m quite prepared to believe that the actual analysis Efron refers to is correct, but a description of it in terms of “getting the prior from the data” isn’t. (By definition, if you got it from the data, it ain’t the prior.)
Matt — Thanks for pointing out the Howson-Urbach book, which I was unaware of. I’ll check it out.
“For those who care, let me state that precisely. In frequentist analyses, all probabilities are of the form P(data | hypothesis), pronounced “the probability that the data would occur, given the hypothesis.” Frequentism flatly refuses to consider probabilities with the hypothesis to the left of the bar — that is, it refuses to consider the probability that any scientific hypothesis is correct.”
This is silly. It is possible to do frequentist statistics using Bayesian methods, and is in fact commonly done. In fact it is what the couple at the begining of the post were doing and what they do at the LHC.
Though I do agree that frequentists who unilaterally reject the use of Bayesian methods are even more silly.
Phil and Ted,
Empirical Bayes is related to hierarchical models. But it’s not as good, so don’t bother learning the former if you know the latter. If you are sloppy with language, hierarchical models can look a bit like using the data to set the prior, but that’s not really true.
Ted: Hierarchical models look like this. If you have parameters theta, but are only comfortable writing the prior conditional on something else (called hyperparameters) alpha, then an inference with alpha included looks like:
p(theta, alpha | D) \propto p(alpha)p(theta|alpha)p(D|theta, alpha) = p(alpha)p(theta|alpha)p(D|theta).
If you marginalise alpha out of this inference, it turns out that the whole thing is just the same as if your prior on theta was p(theta) = \int p(alpha)p(theta|alpha) dalpha.
What did Ed Jaynes get wrong?
I tried making a comment yesterday but it seems to have gotten lost. I’ll try again…
My first point was that empirical Bayes can be seen as an approximation to fully Bayesian hierarchical modeling. Since others have already made this point I won’t belabor it.
My second point was that Efron’s claim that “Bayesian calculations cannot be uncritically accepted and should be checked by other methods, which usually means frequentistically” isn’t meaningless. Many folks who are considered prominent Bayesians advocate “frequentistic” model checking, which typically involves using the fitted model from a Bayesian analysis to simulate synthetic datasets that can then be compared to the observed data. Posterior predictive p-values (aka Bayesian p-values) are computed in this way. Some might argue that such model checking isn’t true to the spirit of Bayesian analysis, but most statisticians I know tend to be more pragmatic and are happy to use Bayesian and frequentist methods depending on the specific applied problem. (I should note that I can’t access Efron’s paper at this time so I’m inferring what I think he means only from the sentence quoted above.)
As a novice, let me ask the following questions.
Let’s go back to your LHC example. Let’s say I consider the model of the Higgs Boson and using frequentist reasoning decide there is a good chance (99.9%) of seeing the data I did if the model were true. I conclude that the Higgs Boson model is probably correct.
How would these conclusions alter if I were to use Bayesian reasoning? Presumably I would still conclude that the Higgs Boson model was correct. Maybe I would not conclude there was a 99.9% probability that the model was correct, but some other probability?
Further to this, let’s assume that after I have done this work someone proposes an alternative model with no HIggs Boson, say SUSY. Let’s say that after a frequentist analysis I decide there is an equally good chance (99.9%) of seeing the data I did if SUSY were true. Because I seem to have two equally valid models I remain agnostic about which one is the correct description of the universe.
Is this situation possible using Bayesian reasoning? Surely I would conclude that both the Higgs Boson model and the SUSY model have a 99.9% chance of being correct given the data, which would be impossible if they were mutually exclusive. I suppose you could update your priors such that each model had a 50% chance of being correct. Then this number would need to be revised each time a competing model was advanced. Surely the frequentist picture has the advantage that the statement it makes about each model remains unchanged as more models are advanced?
Model (hypothesis): person is female. Data: person is pregnant. Probability of data, given model: about 3%. Probability of model, given data: 100%. 🙂 (The prior probability that a woman is pregnant is about 3%.)
I don’t really see how that is analogous with the LHC question.
Model (hypothesis): Higgs Boson exists. Data: 500 counts in 130 GeV channel Probability of data, given model: about 99.9%. Probability of model, given data: ??
To make that calculation in your example you assume a fact about the way the universe is: that only females get pregnant. What do you do with my example, where you can’t reasonably assume that only the Higgs Boson existing would lead to counts in the 130 GeV channel?
In your quoted paragraph that follows “So far so good. Then, a couple of paragraphs later:”, maybe Efron is referring to the invariance problem where a supposedly non-informative prior can be changed (and to an informative one!) simply by reparametrizing the problem.
My source (class lecture notes) also believes Laplace would have chosen the uniform prior for p (in a different example). These brief notes still appear to be publicly available so I refer you to page 7 (“Uniform Priors” and “Invariance” sections) of the PDF here: http://www.stat.duke.edu/~st118/sta732/priors.pdf
“To make that calculation in your example you assume a fact about the way the universe is: that only females get pregnant. What do you do with my example, where you can’t reasonably assume that only the Higgs Boson existing would lead to counts in the 130 GeV channel?”
I’m sure Ted will correct me if I am wrong. I think the key idea is in your last sentence. If you can assume that the Higgs boson is the only reasonable explanation, then the two probabilities are equal. If not, and there are competing hypotheses (other than the null hypothesis, i.e. that the extra counts are just a chance), then the prior probability (based on other experiments, elegance of the theory, reputation of the originator, whatever) comes into play.
Which two probabilities? The frequentist and Bayesian?
Trying to assign numerical values to the elegance of a theory of the reputation of the originator would seem like snake oil to me.
“Which two probabilities? The frequentist and Bayesian?”
No, P(model|data) and P(data|model).
Are you sure? In the example you gave, the only reasonable explanation for a person being pregnant is that they are female, but P(model|data) != P(data|model).
Yes, but the prior probability is 3%.
But you said the prior probability comes into play if this is NOT the case.
(“This” being that there is only one reasonable explanation, either that a person must be female to explain being pregnant or that the Higgs Boson exists to explain counts in the detector channel)
The two cases aren’t directly comparable. If the Higgs boson exists, then a suitably defined experiment should detect it. However, a pregnancy test will indicate pregnancy only if the person is pregnant.
My example was mainly to illustrate, in an obvious way, that the difference between P(model|data) and P(data|model) isn’t some subtle effect, but can make a big difference.
One area where this is commonly abused is the use of DNA testing and quoting probabilities that the suspect is guilty. There are many articles about this particular aspect available online.
I posted this yesterday but it never appeared for some reason. Just a few scattered responses.
What Jaynes got wrong: mostly I think he’s incoherent about the relationship between Bayes and MaxEnt and oversold the latter.
Prob(data|model): e.g. in the LHC discussion above. This will always be a tiny number, because data are complex and there are lots of possible outcomes (before you knew them, afterwards there’s only one!). I believe that this is why Fisher started doing tail areas…to make these probabilities less tiny (and therefore scary).
When the conclusions depend sensitively on the prior: that can happen, and it’s really important to acknowledge it, not sweep it under the rug. If this happens, it’s telling you something really important: the data aren’t very informative, think hard about your prior info and/or get more data!
Great post, Ted. Anecdotally, I can confirm your guess that physicists who use frequentist reasoning are in fact closet Bayesians: updating my mental tally of prior information about which hypotheses are reasonable to test is more or less exactly what I do in day to day work.
Phillip, in what way are the two cases not directly comparable?
Anyway, what does it mean to say “If the Higgs boson exists, then a suitably defined experiment should detect it.”? An experiment is not going to detect the Higgs boson, only have a result that is likely if the Higgs boson exists. Likewise a pregnancy test is only going to give you a result likely if an unborn baby exists.
The root question we’re trying to answer here is “how do you use Bayesian reasoning to tell you the probability that the Higgs Boson exists”?, as the article claimed is possible. Preferably without just stating “Higgs Boson 99% prior, SUSY 1% prior” where the two percentages are completely arbitrary and untestable.
To JH, I think Phillips example would have been better if the model is individual is male and the observation is not pregnant. So the probability of the observation under the model is pretty darn close to 1. Does that mean the individual is male is “probably” true? Or is there still a good chance that the individual is female? The problem is that frequentists can’t say a model is “probably” true because they cannot make probability statements about models.
In your example, forget about SUSY. Let’s say our competing model is that God is fooling around with physicists who are playing with a fancy machine. Well the probability of these high energy observations if God is doing it is probably even greater than the probability of the Higgs Boson model. Congruently, frequentists can never learn anything because all scientific observations are explained by a God with a sense of humor. Or we can use some common sense–or in other words Bayesian inference. Just because the data are consistent with the model does not mean that the model is “probably true”.
Yes, please clarify, enlightened Bayesians: in light of the LHC results, what is the probability that the Higgs Boson exists?
To JH, I think Phillips example would have been better if the model is individual is male and the observation is not pregnant. So the probability of the observation under the model is pretty darn close to 1. Does that mean the individual is male is “probably” true? Or is there still a good chance that the individual is female?”
In that case, the probability of the observation given the model is one, but the probability of the model given the observation is somewhat less than one (because there is a small chance—about one-and-one-half per cent, that the model is a) female and b) pregnant). In this case, the two values don’t differ by much, so people might say that this is just a minor point. In my original example, they differ by a factor of 30.
Phillip, I think the issue is that your example is one in which p(data|model)=small even though p(model|data)=large.
JH had an example that p(data|model)=large and he thought that implied that p(model|data)=large even though it is doubtful he wanted to write that out since it looks bayesian.
Sure, from your example we see that p(data|model)=/=p(model|data) but its probably better to set things up like JH’s premise.
Hence, I thought it was better to come up with an intuitive example that showed p(data|model)=large but we don’t necessarily conclude that the model is true.
“somewhat less than one”
Should be “somewhat greater than one-half”, of course.
Your Venn diagram is fun, but misleading.
The ‘interesting question’ frequentist statistics has always been able to answer is ‘could the effect I’m seeing reasonably be chance?’. That is one of the most important questions a scientist should be asking when trying to test a hypothesis. And it is one of the main reasons frequentist stats has helped science along so much, especially in the more variable sciences.
Where traditional hypothesis testing can mislead is that it only answers half of a research question. It tells you a lot about how well (or poorly) one hypothesis is supported by the data, and hence when to discard a possible explanation, and that remains useful. But it tells you little about how well your particular alternate is supported by the same data.
A good logical framework, Bayesian or not, asks about both sides of the question before settling on the particular alternate. That is why a part of Bayes formula has become so useful in interpreting DNA fingerprint evidence; as we currently use it in the uk, it compares the probability of a match given guilt with the probability of the same match given innocence. (that ratio is sometimes called a likelihood ratio). Interestingly, that comparison does not require a prior; in effect, it is just using two frequentist probabilities. Arguably, that isn’t bayesian at all. But it is still a useful thing to do.
My complaint is that most people who claim they are Bayesian aren’t. (This is not to say they are frequentist or should be.) Many who talk Bayes don’t compute Bayes and most who compute something using Bayes theorem do not use reasonable priors to do so. See my paper “You May Believe you are a Bayesian but you are Probably Wrong” http://www.rmm-journal.de/downloads/Article_Senn.pdf .
In that paper an example from Howson and Urbach’s book is considered. This is an example where they make a claim about what the correct Bayesian inference is but they haven’t done the maths and when you do there is a surprise in store.
I must respectfully disagree with S Ellison. I deny that frequentist methods ever answer the question “Could the effect I’m seeing reasonably be chance?” They certainly don’t do so without folding in a prior — that is, without invoking Bayesian reasoning.
Take the old, familiar example. You test positive for a disease. Frequentist methods tell you that the test has a 0.1% failure rate — that is, only 0.1% of people who don’t have the disease test positive “by chance.” That absolutely does not mean that there’s a 0.1% chance that the effect that you’re seeing has a 0.1% probability of being due to chance. If the disease is sufficiently rare, then the probability that you’re seeing a chance fluctuation (that the null hypothesis is correct, in other words) can be arbitrarily high.