Oddly enough, I still read the Sunday New York Times on paper. As a result, I was extremely confused by George Johnson’s article headlined Gamblers, Scientists, and the Mysterious Hot Hand.
The heart of the article is this claim:
In a study that appeared this summer, Joshua B. Miller and Adam Sanjurjo suggest why the gambler’s fallacy remains so deeply ingrained. Take a fair coin — one as likely to land on heads as tails — and flip it four times. How often was heads followed by another head? In the sequence HHHT, for example, that happened two out of three times — a score of about 67 percent. For HHTH or HHTT, the score is 50 percent.
Altogether there are 16 different ways the coins can fall. I know it sounds crazy but when you average the scores together the answer is not 50-50, as most people would expect, but about 40-60 in favor of tails.
Maybe it’s just me, but I couldn’t make sense of this claim. The online version has a graphic that clears it up. The last sentence is literally correct (with the possible exception of the phrase “as most people would expect,” as I’ll explain), but I couldn’t manage to parse it. I wonder if it was just me.
Here’s my summary of exactly what is being said:
Suppose you flip a coin four times. Every time heads comes up, you look at the next flip and see if it’s heads or tails. (Of course, you can’t do this if heads comes up on the last flip, since there is no next flip.) You write down the fraction of the time that it came up heads. For instance, if the coin flips went HHTH, you’d write down 1/2, because the first H was followed by an H, but the second H was followed by a T.
You then repeat the procedure many times (each time using a sequence of four coin flips). You average together all the results you get. The average comes out less than 1/2.
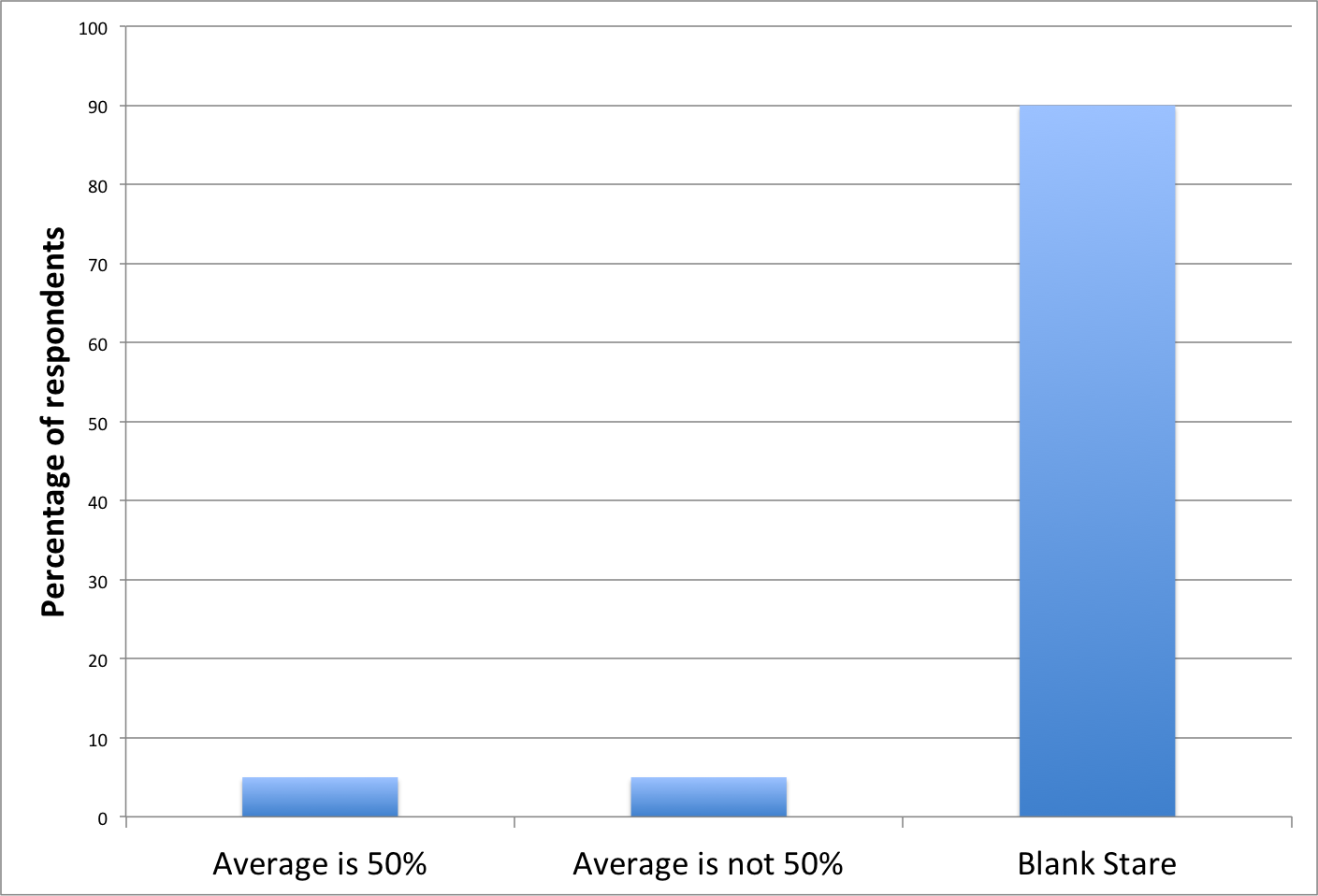
I guess that might be a counterintuitive result. Maybe. Personally, I find the described procedure so baroque that I’m not sure I would have had any intuition at all as to what the result should be. Hence my skepticism about the “as most people would expect” phrase. I think that if you took a survey, you’d get something like this:
(And, by the way, I don’t mean this as an insulting remark about the average person’s mathematical skills: I think I would have been in the 90%.)
The reason you don’t get 50% from this procedure is that it weights the outcomes of individual flips unevenly. For instance whenever HHTH shows up, the HH gets an effective weight of 1/2 (because it’s averaged together with the HT). But in each instance of HHHH, each of the three HH’s gets an effective weight of 1/3 (because there are three of them in that sequence). The correct averaging procedure is to count all the individual instances of the things you’re looking for (HH’s); not to group them together, average those, and then average the averages.
My question is whether the average-of-averages procedure described in the article actually corresponds to anything that any actual human would do.
The paper Johnson cites (which, incidentally, is an non-peer-reviewed working paper) makes grandiose claims about this result. For one thing, it is supposed to explain the “gambler’s fallacy.” Also, supposedly some published analyses of the “hot hands” phenomenon in various sports are incorrect because the authors used an averaging method like this.
At some point, I’ll look at the publications that supposedly fall prey to this error, but I have to say that I find all this extremely dubious. It doesn’t seem at all likely to me that that bizarre averaging procedure corresponds to people’s intuitive notions of probability, nor does it seem likely that a statistician would use such a method in a published analysis.
But he writes “If the analysis is correct, the possibility remains that the hot hand is real.” which I think is wrong, not just strangely worded, at least for the standard definition of “hot hand”.
I had also failed to parse the original sentence, and only made sense of what was being said after reading your summary. I agree that this is a funny calculation to attempt, because of the way in which the counting is done, though the example I would pick to illustrate this discomfort is the counting tails gets on your example
HHTH : 0.5
while in the symmetrically ‘opposite’ seuqence
TTHT: heads seems to get 0, if I understand the prescription.
The most perplexing moment for me was
“For a 50 percent shooter, for example, the odds of making a basket are supposed to be no better after a hit — still 50-50. But in a purely random situation, according to the new analysis, a hit would be expected to be followed by another hit less than half the time.”
Does the “new analysis” change the definition of “purely random” for a 50-50 shooter? Maybe I’m missing something about the argument the author makes, but it seems he is misunderstanding the meaning of independent events. For a 50-50 shooter, in a purely random situation, a hit would be expected to be followed by — well, the hit would be forgotten.
The gambler’s fallacy is simple, can be explained in a couple of sentences, and I don’t believe there’s anything deeper there (mathematically). Thinking too hard about things can get one into trouble. I believe the author may be suffering from a similar affliction gamblers suffer from: thinking too hard about what he really should know is completely random!
I have another issue with this. I realized the gambler’s fallacy operates both ways, somehow unlike the argument made in the article. Oh, also, betting’s involved. So, what if you repeated the flip-coins-4-times experiment, showing all the possible outcomes of 4 coin flips. Suppose you, as a foolish gambler, simply bet every time that the coin would show the opposite of whatever you just saw. Across all 16 possible outcomes, a total of 48 bets are made and 24 are winners: 50-50.
Perhaps it’s more like an actual foolish gambler to wait until a streak’s observed to bet, e.g. wait for Red-Red in roulette, then bet on Black. Or vice versa. Doing this in the coin example leads to 16 bets made, with 8 being winners. Again, 50-50.
This seems to me more like what an actual person would do.
Sorry for all the comments, but I’m going to be rich! If instead of tallying the 16 bets made, with 8 winners, I instead calculate the proportion of won bets in each of the 16 possible sequences of four coin flips, and then average THOSE, I don’t get 50-50, as expected. Instead I get 58.3% !
Older readers here might remember Jimmy The Greek. He was a professional gambler. In Vegas, he didn’t play the games, though. He made side bets like “I bet you a thousand that that guy who just put a million on black at roulette won’t win”. As every professional gambler knows, the house always wins in the long term, so Jimmy was wise in that he didn’t play against the house, but against customers.
Hi Ted
just came across your two posts on google. I posted a note on your other post.
The statistic is computed for a single sequence, and the test is performed for a single player, so it it more natural than described here.
There is no analysis of an average of ratios.
We have a primer that addresses your concerns, here it is:
http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2728151
In the box headed “Not Really A Toss-Up,” there is a column of ratios (100%,67%,…), which are then averaged. That’s an average of ratios.
That box purports to be an explanation of the argument in the working paper. If it’s not, then you should urge the New York Times to publish a correction.