Category: Uncategorized

You can come hear me give a talk on “Listening to the Big Bang” at the Science Museum of Virginia this coming Wednesday at noon.  It’s part of their Lunch Break Science series.

As the UR faculty representative for the Goldwater Scholarship, I want to congratulate MattDer, Sally Fisher, and Anna Parker, for the outstanding work in class and in their research labs that led to their selection as UR’s nominees this award.  If you see them, congratulate them on their excellent work preparing their applications.

Update: I originally said Brian Der instead of Matt Der, which was wrong on two counts: The actual nominee is Matt, and Matt’s brother Bryan (a past Goldwater winner) spells his name with a Y anyway.  Sorry to both Ders!

As I keep mentioning ad nauseam, I think probability’s really important in understanding all sorts of things about science.  Here’s a really basic question that’s easy to ask but maybe not so easy to answer: What do probabilities mean anyway?

Not surprisingly, this is a question that philosophers have taken a lot of interest in.  Here’s a nice article reviewing a bunch of interpretations of probability.   The article lists a bunch of different interpretations, but ultimately I think the most important distinction to draw is between objective and subjective interpretations: Are probabilities statements about the world, or are they statements about our knowledge and belief about the world?

The poster child for the objective interpretation is frequentism, and the main buzzword associated with the subjective interpretation is Bayesianism.  If you’re a frequentist, you think that probabilities are descriptions of the frequency with which a certain outcome will occur in many repeated trials of an experiment.  If you want to talk about thing that don’t have many repeated trials (e.g., a weatherman who wants to say something about the chance of rain tomorrow, or a bookie who wants to set odds for the next Super Bowl), then you have to be willing to imagine many hypothetical repeated trials.

The frequentist point of view strikes me as so utterly bizarre that I can’t understand why anyone takes it seriously.  Suppose that I say that the Red Sox have a 20% chance of winning the World Series this year. Can anyone really believe that I’m making a statement about a large (in principle infinite) number of imaginary worlds, in some of which the Red Sox win and in others of which they lose?  And that if Daisuke Matsuzaka breaks his arm tomorrow, something happens to a bunch of those hypothetical worlds, changing the relative numbers of winning and losing worlds? These sound utterly crazy to me, but as far as I can tell, frequentists really believe that that’s what probabilities are all about.

It seems completely obvious to me that, when I say that the Red Sox have a 20% chance of winning the World Series, I’m describing my state of mind (my beliefs, knowledge, etc.), not something about a whole bunch of hypothetical worlds.  That makes me a hardcore Bayesian.

So here’s what I’m wondering. Lots of smart people seem to believe in a frequentist idea of probability.  Yet to me the whole idea seems not just wrong, but self-evidently absurd.  This leads me to think maybe I’m missing something. (Then again, John Baez agrees with me on this, which reassures me.)  So here’s a question for anyone who might have read this far: Do you know of anything I can read that would help me understand why frequentism is an idea that even deserves a serious hearing?

In my experience, most scientists don’t know or care much about the philosophy of science, but if they do know one thing, it’s Karl Popper’s idea that the hallmark of a scientific hypothesis is falsifiability.  In general, scientists seem to have taken this idea to heart.  For instance, when a scientist wants to explain why astrology, or Creationism, or any number of other things aren’t science, the accusation of unfalsifiability invariably comes up.  Although I’ll admit to using this rhetorical trick myself from time to time, to me the idea of falsifiability fails in a big way to capture the scientific way of thinking.  I hinted about this in an earlier post, but now I’d like to go into it in a bit more detail.

Let me begin with a confession: I have never read Popper.  For all I know, the position I’m about to argue against is not what he really thought at all.  It is of course a cardinal academic sin to argue against someone’s position without  actually knowing what that person wrote.  My excuse is that I’m going to argue against Popper as he is generally understood by scientists, which may be different from the real Popper.  As a constant reminder that I may be arguing against a cartoon version of Popper, I’ll refer to cartoon-Popper as “Popper” from now on.  (If that’s not showing up in a different font on your browser, you’ll just have to imagine it.  Maybe you’re better off.)

I bet that the vast majority of scientists, like me, know only Popper‘s views, not Popper’s views, so I don’t feel too bad about addressing the former, not the latter.

Popper‘s main idea is that a scientific hypothesis must be falsifiable, meaning that it must be possible for some sort of experimental evidence to prove the hypothesis wrong.  For instance, consider the “Matrix-like” hypothesis that you’re just a brain in a vat, with inputs artificially pumped in to make it seem like you’re sensing and experiencing all of the things you think you are.  Every experiment you can imagine doing could be explained under this hypothesis, so it’s not falsifiable, and hence not scientific.

When Popper says that a scientific hypothesis must be falsifiable, it’s not clear whether this is supposed to be a descriptive statement (“this is how scientists actually think”) or a normative one (“this is how scientists should think”).  Either way, though, I think it misses the boat, in two different but related ways.

1. Negativity.  The most obvious thing about Popper‘s falsifiability criterion is that it privileges falsifying over verifying. When scientists talk about Popper, they often regard this as a feature, not a bug.  They say that scientific theories can never be proved right, but they can be proved wrong.

At the level of individual hypotheses, this is self-evidently silly.  Does anyone really believe that “there is life on other planets” is an unscientific hypothesis, but “there is no life on other planets” is scientific?   When I write a grant proposal to NSF, should I carefully insert “not”s in appropriate places to make sure that the questions I’m proposing to address are phrased in a suitably falsifiable way?  It’d be like submitting a proposal to Alex Trebek.

From what little I’ve read on the subject, I think that this objection is about Popper, not Popper, in at least one way.  The real Popper apparently applied the falsifiability criterion to entire scientific theories, not to individual hypotheses.  But it’s not obvious to me that that helps, and anyway Popper as understood by most scientists is definitely about falsifiability of individual hypotheses. For example, I was recently on a committee to establish learning outcomes for our general-education science courses as part of our accreditation process.  One of the outcomes had to do with formulating scientific hypotheses, and we discussed whether to include Popperian falsifiability as a criterion for these hypotheses.  (Fortunately, we decided not to.)

2. “All-or-nothing-ness.” The other thing I don’t like about Popperian falsifiability is the way it thinks of hypotheses as either definitely true or definitely false. (Once again, the real Popper’s view is apparently more sophisticated than Popper‘s on this point.) This problem is actually much more important to me than the first one.  The way I reason as a scientist places much more emphasis on the uncertain, tentative nature of scientific knowledge: it’s crucial to remember that beliefs about scientific hypotheses are always probabilistic.

Bayesian inference provides a much better model for understanding both how scientists do think and how they should think.  At any given time, you have a set of beliefs about the probabilities of various statements about the world being true.  When you acquire some new information (say by doing an experiment), the additional information causes you to update those sets of probabilities.  Over time, that accumulation of evidence drives some of those probabilities very close to one and others very close to zero.  As I noted in my earlier post,Bayes’s theorem provides a precise description of this process.

(By the way, scientists sometimes divide themselves into “frequentist” and “Bayesian” camps, with different interpretations of what probabilities are all about.  Some frequentists will reject what I’m saying here, but I claim that they’re just in denial: Bayesian inference still describes how they reason, even if they won’t admit it.)

For rhetorical purposes if nothing else, it’s nice to have a clean way of describing what makes a hypothesis scientific, so that we can state succinctly why, say, astrology doesn’t count.  Popperian falsifiability nicely meets that need, which is probably part of the reason scientists like it.  Since I’m asking you to reject it, I should offer up a replacement.  The Bayesian way of looking at things does supply a natural replacement for falsifiability, although I don’t know of a catchy one-word name for it.  To me, what makes a hypothesis scientific is that it is amenable to evidence.  That just means that we can imagine experiments whose results would drive the probability of the hypothesis arbitrarily close to one, and (possibly different) experiments that would drive the probability arbitrarily close to zero.

If you write down Bayes’s theorem, you can convince yourself that this is equivalent to the following:  a hypothesis H is amenable to evidence as long as there are some possible experimental results E with the property that P(E | H) is significantly different from P(E | not-H).  That is, there have to be experimental outcomes that are much more (or less) likely if the hypothesis is true than if it’s not true.

Most examples of unscientific hypotheses (e.g., astrology) fail this test on the ground that they’re too vague to allow decent estimates of these probabilities.

The idea of evidence, and the amenability-to-evidence criterion, are pretty intuitive and not too hard to explain:  “Evidence” for a hypothesis just means an observation that is more consistent with the hypothesis being true than with its being false.  A hypothesis is scientific if you can imagine ways of gathering evidence.  Isn’t that nicer than Popperian falsifiability?

I don’t read much business journalism, but I do generally like Joe Nocera’s writing in the New York Times.  I thought his long article on risk management in last Sunday’s Times Magazine was quite good.  In particular, I love seeing an article in a nontechnical magazine that actually talks about probability distributions in a reasonably careful and detailed way.  If you want to understand how to think about data, you’ve got to learn to love thinking about probabilities.

The hero, so to speak, of the article is Nassim Nicholas Taleb, author of the book The Black Swan.  According to the article, he’s been trying to convince people of the inadequacies of a standard risk-assessment method for many years, mostly because the method doesn’t pay attention to the tails of the probability distribution.  The standard method, called VaR, is meant to give a sort of 99% confidence estimate of how much money a given set of investments is at risk of losing.  Taleb’s point, apparently, is that even if that’s right it doesn’t do you all that much good, because what really matters for risk assessment is how bad the other 1% can be.

That’s an important point, which comes up in other areas too.  When people compare health insurance plans, they look at things like copays, which tell you what’ll happen under more or less routine circumstances.  It seems to me that by far the more important think to pay attention to in a health plan is how things will play out in the unlikely event that you need, say, a heart transplant followed by a lifetime of anti-rejection drugs.  (In fact, extreme events like these are the reason you want insurance at all: if all you were going to need was routine checkups and the like, you’d be better off going without insurance, investing what you would have spent on premiums, and paying out of pocket.)

I do have a couple of observations about the article:

1. Nocera, quoting Taleb, keeps referring to the problem as the “fat tails” of the probability distribution.  I think he means “long tails,” though, which is pretty much the opposite.  A probability distribution with fat tails would be one in which moderately extreme outcomes were more likely than you might have expected.  That wouldn’t be so bad.  A distribution with long tails is one in which very very extreme outcomes have non-negligible probabilities.  The impression I get from the rest of the article is that this is the problem that Taleb claims  is the source of our woes.

2. The article is strong on diagnosis, but I wish it had said more about treatment.  Given that standard methods don’t handle the tails very well, what should risk-management types do about it?  I fear that the article might leave people with the impression that there’s no way to fix methods like VaR to take better account of the tails, and that we shouldn’t even bother trying to quantify risk with probability theory.  That’s certainly not the correct conclusion: There’s no coherent way to think about risk except by modeling probability distributions.  If the existing models aren’t good enough, we need better models.  I hope that smart quants are thinking about this, not just giving up.

3. Taleb seems like he’s probably very smart and is certainly not a nice guy.

I just sent a note off to Will Shortz about an error in the NY Times crossword puzzle.  Here’s what I said.

Pretty much every time that I think I've noticed an error in the Times crossword, the error turns out to be mine.  But as a physicist and physics teacher, I'm confident about this one.  In Saturday's puzzle, 59 down is defined as "Energy expressed in volts: Abbr.", and the answer is "EMF".  This definition is incorrect.  An EMF is generally expressed in volts, but it's not an energy.  In fact, the volt isn't even a unit of energy, so "energy expressed in volts" is sort of like "distance expressed in pounds" or "speed expressed in dollars."

EMF is a form of voltage, or equivalently of electric potential (these two are synonyms).  Another way to say it is "energy per charge", but that "per charge" part is very important.  For instance, a car battery supplies an emf of 12 V, which is less than the emf of a pair of 9-volt batteries.  But despite the relatively small emf, the car battery has a lot more energy stored in it than the two 9-volts.

By the way, you probably don't remember me, but we spoke on the phone about 10 years ago: I was an on-air participant in the NPR puzzle.  You stumped me with "Pal Joey", but other than that I did OK.

By the way, emf is a good candidate for the most misleading name in physics: the F stands for “force”, but in addition to not being an energy, emf isn’t a force either.  At least one textbook (I can’t remember which) says that you shouldn’t think of EMF as standing for anything, putting it in the same category as  KFC and the AARP.  (The Oakland A’s used to be in this category too, but I think they’re not anymore.)

I wrote up the argument of my last post a bit more carefully and sent it off to the American Journal of Physics as a comment on the original article by Styer.  Here’s a PDF of the submitted version.  I tried to clean up the argument and fill in some gaps, but nothing substantial has changed.

There’s an interesting article by Daniel Styer in the November 2008 issue of the American Journal of Physics.  The full article is behind a subscription wall, so if you’re not a subscriber you can’t see it.  The link should take you to the title and abstract, but in case it doesn’t, here they are:

Daniel Styer, “Entropy and Evolution,” American Journal of Physics, 76, 1031-1033 (November 2008).

Abstract: Quantitative estimates of the entropy involved in biological evolution demonstrate that there is no conflict between evolution and the second law of thermodynamics. The calculations are elementary and could be used to enliven the thermodynamics portion of a high school or introductory college physics course.

The article addresses a claim often made by creationists that the second law of thermodynamics is inconsistent with evolution.  The creationist argument goes like this: The second law of thermodynamics says that entropy always increases, which means that things always progress from order to disorder.  In biological evolution, order is created from disorder, so it is contradicted by the second law.

The creationist argument is wrong.  It rests on misunderstandings about what the second law of thermodynamics actually says.  Debunkings of the argument can be found in a bunch of places.  The point of Styer’s article is to assess quantitatively just how wrong it is.  This is a worthy goal, but Styer makes a mistake in his analysis that seriously distorts the physics. I feel a little bad about even mentioning this. After all, Styer is on the side of the (secular) angels here, and his final conclusion is certainly right: the creationists’ argument is without merit.  Fortunately, as I’ll show, Styer’s mistake can be fixed in a way that demonstrates this unambiguously.

This post is kind of long, so here’s the executive summary:

1. The creationists’ argument that evolution and the second law are incompatible rests on misunderstandings.   (This part is just the conventional view, which has been written about many times before.)
2. Styer’s attempt to make this point more quantitative requires him to guess a value for a certain number.  His guess is a wild underestimate, causing him to underestimate the amount of entropy reduction required for evolution and making his argument unpersuasive.  The reason it’s such a huge underestimate is at the heart of what statistical mechanics is all about, which is why I think it’s worth trying to understand it.
3. We can fix up the argument, estimating things in a way that is guaranteed to overstate the degree of entropy reduction required for evolution.  This approach gives a quantitative and rigorous proof that there’s no problem reconciling evolution and the second law.

The conventional wisdom.  The main reason that the creationist argument is wrong is that the second law applies only to thermodynamically closed systems, that is to say to systems with no heat flow in or out of them.  Heat is constantly flowing into the Earth (from the Sun), and heat is constantly escaping from the Earth into space, so the Earth is not a thermodynamically closed system.  When you’re dealing with a system like that, the way to apply the second law is to think of the system you’re considering as part of a larger system that is (at least approximately) closed.  Then the second law says that the total entropy of the whole big system must increase.  It does not forbid the entropy of one subsystem from decreasing, as long as other parts increase still more.  In fact, when heat flows from a very hot thing (such as the Sun) to a colder thing (such as the Earth), that heat flow produces a huge increase in entropy, and as a result it’s very easy for decreases in entropy to occur in the rest of the system without violating the second law.

Imagine raking the leaves in your yard into a pile.  The entropy of a localized pile of leaves is less than the entropy of the leaves when they were evenly spread over your yard.  You managed to decrease that entropy by expending some energy, which was dissipated in the form of heat into the environment.  That energy dissipation increased the total entropy by more (much, much more, as it turns out) than the decrease in the entropy of the leaves.

There is a second reason the creationist argument is wrong, which is that entropy is not exactly the same thing as disorder.  Often, entropy can be thought of as disorder, but that correspondence is imperfect.  It seems clear that in some sense a world with lots of organism in it is more “organized” than a world with just a primordial soup, but the exact translation of that vague idea into a statement about entropy is tricky.  The first reason (Earth is not a closed system) is much more important, though.

The main purpose of Styer’s article is to quantify these points. In particular, he quantifies the amount of entropy supplied by sunlight on the Earth and the amount of entropy decrease supposedly required for biological evolution.  The point is to show that the first number is much greater than the second, and so there’s no problem reconciling the second law and evolution.

What’s wrong with Styer’s argument.  The problem with his argument comes in Section III, in which he tries to estimate the change in entropy of living things due to evolution:

Suppose that, due to evolution, each individual organism is 1000 times “more improbable” than the corresponding individual was 100 years ago.  In other words, if Ω_i is the number of microstates consistent with the specification of an organism 100 years ago, and Ω_f is the number of microstates consistent with the specification of today’s “improved and less probable” organism, then Ω_f =  10^-3Ω_i. I regard this as a very generous rate of evolution, but you may make your own assumption.

Thanks!  I don’t mind if I do.

1000 is a terrible, horrible, ridiculous underestimate of this “improbability ratio.”  The reason gets at the heart of what statistical mechanics is all about. One of the most important ideas of statistical mechanics is that probability ratios like this, for macroscopic systems, are almost always exponentially large quantities.  It’s very hard to imagine anything you could do to a system as large as, say, a cell, that would change the number of available microstates (generally known as the “multiplicity”) by a mere factor of 1000.

If a single chemical bond is broken, for instance, then energy of about E=1 eV is absorbed from the system, reducing the multiplicity by a factor of about e^E/kT, or about 10¹⁷ at typical biological temperatures.  That’s not the sort of thing Styer is talking about, of course: he’s talking about the degree to which evolution makes things “more organized.”  But changes of that sort always result in  reductions in multiplicity that are at least as drastic.  Let me illustrate with an example. [The fainthearted can feel free to skip the next paragraph — just look at the large numbers in the last couple of sentences.]

Suppose that the difference between an organism now and the same organism 100 years ago is that one additional protein molecule has formed somewhere inside the organism.  (Not one kind of protein — one single molecule.)  Suppose that that protein contains 20 amino acids, and that those amino acids were already present in the cell in the old organism, so that all that happened was that they got assembled in the right order.  That results in an enormous reduction of multiplicity: before the protein formed, the individual amino acids could have been anywhere in the cell, but afterwards, they have to be in a specific arrangement. A crude estimate of the multiplicity reduction is just the degree to which the multiplicity of a dilute solution of amino acids in water goes down when 19 amino acids are taken out of it (since those 19 have to be put in a certain place relative to the 20th).  The answer to that question is e^-19μ/kT, where μ is the chemical potential of an amino acid.  Armed with a statistical mechanics textbook [e.g., equation (3.63) of the one by Schroeder that I’m currently teaching from], you can estimate the chemical potential.  Making the most pessimistic assumptions I can, I can’t get -μ/kT below about 10, which means that producing that one protein reduces the multiplicity of the organism (that is, makes it more “improbable”) by a factor of at least 10⁸⁰ or so (that’s e^-190).  And that’s to produce one protein.  If instead we imagine that a single gene gets turned on and produces a bunch of copies of this protein, then you have to raise this factor to the power of the number of protein molecules created.

That calculation is based on a bunch of crude assumptions, but nothing you do to refine them is going to change the fact that multiplicity changes are always by exponentially large factors in a system like this.  Generically, anything you do to a single molecule results in multiplicity changes given by  e^-μ/kT, μ is always at least of order eV, and kT is only about 0.025 eV.  So the ante to enter this game is something like e⁴⁰, or 10¹⁷.

Fixing the problem.  It’s been a few paragraphs since I said this, so let me say it again: Despite this error, the overall conclusion that there is no problem with evolution and the second law of thermodynamics is still correct.  Here’s a way to see why.

Let’s make an obviously ridiculous overestimate of the total entropy reduction required to create life in its present form on Earth.  Even this overestimate is still far less than what we get from the Sun.

Suppose that we started with a planet exactly like Earth, but with no life on it.  I’ll call this planet “Dead-Earth.” The difference between Dead-Earth and actual Earth is that every atom in the Earth’s biomass is in Dead-Earth’s atmosphere in its simplest possible form.  Now imagine that an omnipotent being (a Maxwell’s demon, if you like) turned Dead-Earth into an exact replica of Earth, with every single molecule in the position that it’s in right now, by plucking atoms from the atmosphere and putting them by hand into the right place.  Let’s estimate how much that would reduce the entropy of Dead-Earth.  Clearly the entropy reduction required to produce an exact copy of life on Earth is much less than the entropy reduction required to produce life in general, so this is an overestimate of how much entropy reduction the Sun has to provide us.

Earth’s total biomass has been estimated at 10¹⁵ kg or so, which works out to about 10⁴¹ atoms.  The reduction in multiplicity when you pluck one atom from the atmosphere and put it into a single, definite location is once again  e^-μ/kT . This factor works out to at most about e¹⁰.  [To get it, use the same equation as before, (3.63) in Schroeder’s book, but this time use values appropriate for the simple molecules like N₂ in air, not for amino acids in an aqueous solution.]  That means that putting each atom in place costs an amount of entropy ΔS = 10k where k is Boltzmann’s constant.  To put all 10⁴¹ atoms in place, therefore, requires an entropy reduction of 10⁴²k.

Styer calculates (correctly) the amount of entropy increase caused by the throughput of solar energy on Earth, finding it to be of order  10³⁷k every second.  So the Sun supplies us with enough entropy every 100,000 seconds (about a day) to produce all of life on Earth.

The conclusion: Even if we allow ourselves a ridiculous overestimate of the amount of entropy reduction associated with biological evolution, the Sun supplies us with enough entropy to evolve all of life on Earth in just a couple of days (six days, if you like).

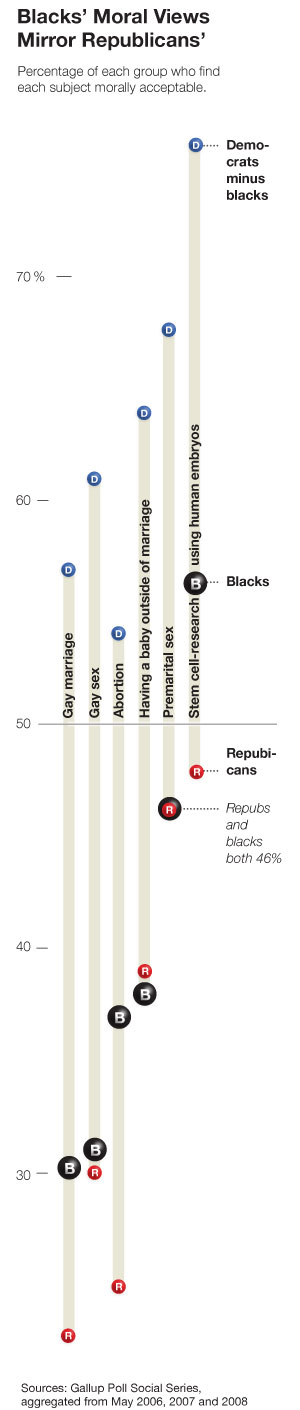
 There’s a very confusing graphic in today’s New York Times:

Take the last column for instance.  It seems to say that the approval rating among blacks is 57%, and the difference between democrats and blacks is 77%.  By using the sophisticated mathematical identity

(democrats – blacks) + blacks = democrats,

I find that 134% of democrats approve of stem cell research.

Is just an editing error?  Should the label “democrats minus blacks”  just read “democrats”?  That’s the only way I can make sense of it.

As long as I’m here, I’ll whine a bit more about the Times’s choice of graphics.  The Times magazine usually runs a small chart to illustrate a point related to the first short article in the magazine.  It’s clear that the editor has decided that making the graph interesting-looking is more important than making it convey information.  Here’s a particularly annoying example:

If you wanted to design a way to hide the information in a graphic, you couldn’t do much better than this.  The whole point of the pie slices is to allow a comparison of the areas, and they’re drawn in a perspective that almost perfectly hides the areas from view.  Where’s Edward Tufte when you need him?

My recent post about Blacklight Power’s claim that there’s a lower-energy state of hydrogen (which they call a hydrino) seems to have gotten a bit of interest — at least enough to show that this blog isn’t completely a form of write-only memory. I want to follow up on it by explaining in a bit more detail why I’m so skeptical of this claim.  In the process, I’ll say a bit about Bayesian inference.  The idea of Bayesian inference is, in my opinion, at the heart of what science is all about, and it’s a shame that it’s not talked about more.

But before we get there, let me summarize my view on hydrinos.  If Randell Mills (the head of Blacklight Power, and the main man behind hydrinos) is right, then the best-tested theory in the history of science is not merely wrong, but really really wrong.  This is not a logical impossibility, but it’s wildly unlikely.

Let me be more precise about the two italicized phrases in the previous paragraph.

1. “The best-tested theory in the history of science.”  The theory I’m talking about is quantum physics, more specifically the quantum mechanics of charged  particles interacting electromagnetically, and even more specifically the theory of quantum electrodynamics (QED).  Part of the reason for calling it the best-tested theory in science is some amazingly high-precision measurements, where predictions of the theory are matched to something like 12 decimal places.  But more important than that are the tens of thousands of experiments done in labs around the world all the time, which aren’t designed as tests of QED, but which depend fundamentally on QED.

Pretty much all of atomic physics and most of solid state physics (which between them are a substantial majority of physics research) depends on QED.  Also, every time an experiment is done at a particle accelerator, even if its purpose is to test other physics, it ends up testing QED. This has been true for decades.  If there were a fundamental flaw in QED, it is inconceivable that none of these experiments would have turned it up by now.

2. “Really really wrong.“  There’s a hierarchy of levels of “wrongness” of scientific theories.  For instance, ever since Einstein came up with general relativity, we’ve known that Newton’s theory of gravity was wrong: in some regimes, the two theories disagree, and general relativity is the one that agrees with experiment in those cases.  But Newtonian gravity is merely wrong, not really really wrong.

It’s intuitively clear that there’s something deeply “right” about Newtonian gravity — if there weren’t, how could NASA use it so successfully (most of the time) to guide space probes to other planets?  The reason for this is that Newtonian gravity was subsumed, not replaced, by general relativity.  To be specific, general relativity contains Newtonian gravity as a special limiting case.  Within certain bounds, Newton’s laws are a provably good approximation to the more exact theory.  More importantly, the bedrock principles of Newtonian gravity, such as conservation of energy, momentum,  and mass, have a natural place in the broader theory.  Some of these principles (e.g., energy and momentum conservation) carry over into exact laws in the new theory.  Others (mass conservation) are only approximately valid within certain broad limits.

So Newtonian gravity is an example of a theory that’s wrong but not really really wrong.  I would describe a theory as really really wrong if its central ideas were found to be not even approximately valid, in a regime in which the theory is well-tested.  The existence of hydrinos would mean that QED was really really wrong in this sense.  To be specific, it would mean that bedrock principles of quantum physics, such as the Heisenberg uncertainty principle, were not even approximately valid in the arena of interactions of electrons and protons at length scales and energy scales of the order of atoms.  That’s an arena in which the theory has been unbelievably well tested.

There has never been an instance in the history of science when a theory that was tested even 1% as well as QED was later proved to be really really wrong.  In fact, my only hesitation in making that statement is that it’s probably a ridiculous understatement.

So what?  In the cartoon version of science, even one experiment that contradicts a theory proves the theory to be wrong.  If Randell Mills has done his experiment right, then quantum physics is wrong, no matter how many previous experiments have confirmed it.

The problem with this cartoon version is that results of experiments are never 100% clear-cut.  The probability that someone has made a mistake, or misinterpreted what they saw, might be very low (especially if an experiment has been replicated many times and many people have seen the data), but it’s never zero.  That means that beliefs about scientific hypotheses are always probabilistic beliefs.

When new evidence comes in, that evidence causes each person to update his or her beliefs about the probabilities of various hypotheses about the world.  Evidence that supports a hypothesis causes us to increase our mental probability that that hypothesis is true, and vice versa. All of this sounds obvious, but it’s quite different from the black-and-white cartoon version that people are often taught.  (I’m looking at you, Karl Popper.  Falsifiability?  Feh.)

All of this brings us at last to Bayesian inference.  This is the systematic way of understanding the way that probabilities get updated in the light of new evidence.

Bayes’s Theorem relates  a few different probabilities to each other:

• The posterior probability P(H | E),  which is the probability that a hypothesis is true, given an experimental result.
• The prior probability P(H), which is the probability that the hypothesis is true, without considering that experimental result.
• The evidence P(E | H), which is the probability that the experimental result would have occurred, assuming that the hypothesis is true.

The prior and posterior probabilities are your subjective assessments of the likelihood of the hypothesis, before and after you saw the experimental result.  Bayes’s Theorem tells you quantitatively how different the posterior probability is from the prior probability — that is, how much you’ve changed your mind  as a result of the new experiment.  Specifically, the theorem says that an experiment that supports a hypothesis (that is, one in which P(E|H) is large) causes you to raise your estimate of the probability of the hypothesis being correct, while an experiment that contradicts the hypothesis (one with a low value of P(E|H)) causes you to reduce it.

Here’s the thing:  in situations where the prior probability was already very large or very small, the posterior probability tends not to change very much unless the evidence is similarly extreme.  For example, say the hypothesis is that quantum physics is not really really wrong.  Before I’d ever heard of Randell Mills, the prior probability of that hypothesis was extremely high (because of the accumulation of nearly a century of experimental evidence).  Let’s put it at 0.999999 (although that’s actually way too low).  Now let’s suppose that Mills has done his experiment really well, so that there’s only a one in ten thousand chance that he’s made a mistake or misinterpreted his results.  That means that the evidence (the probability that quantum physics is OK given his results) is only 0.0001. If you put those numbers into Bayes’s theorem and turn the crank, you find that the posterior probability is still 99%.  That is, even if I have very high confidence in the quality of the experiment, the overwhelming prior evidence means that I’ll still think it’s probably wrong.

A good analogy here is the probability of getting a false positive result in a test for a rare disease: Even if the test has a very low rate of false positives, if the disease is sufficiently rare your positive result has a high probabliity of being false.

All of this is just a long-winded way of talking about the old scientific maxim that extraordinary claims require extraordinary evidence. The nice thing about it is that it’s also quantitative: it tells you how extraordinary the evidence must be.