The August 2011 issue of the American Journal of Physics (paywalled, I assume) has two articles about nice physics puzzles. The statement of these puzzles should be understandable to people who know university-level introductory physics, but the solutions are hard.
Here’s the first one. I’ll put the second in another post.
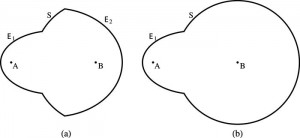
Suppose you have a strangely-shaped perfectly reflecting cavity like the one in Figure (a) below. The surface consists of parts of two ellipsoids and one sphere. The ellipsoids have foci A and B, and the sphere’s center is at B. Any light ray leaving point A hits part of an ellipsoid and ends up at B. Some light rays leaving B hit ellipsoids and end up at A, while others hit the sphere and go back to B.
Now put objects (blackbodies) at points A and B. They both radiate. All of the radiation from A heats up B, but only some of the radiation from B heats up A. So if the two bodies start out at the same temperature, there’ll be a net energy flow from A to B. But that violates the second law of thermodynamics. What’s going on?
In real life, such a system wouldn’t obey ray optics — the radiation would diffract around, eventually filling the volume of the cavity. Also, the walls wouldn’t really be perfectly reflective, so they’d heat up and radiate themselves. But I don’t think those considerations count as resolutions of the paradox: we can certainly imagine a world in which ray optics works and reflection work perfectly, and the second law should hold in such a world.
Someone told me this puzzle back when I was in grad school, and it bothered me for a while. Eventually, I think I hit on the same answer as the one in the AJP article.
I’m assuming that in the Abstract, the phrase “the finite sizes of the black bodies” should be changed to “the >nonzero< sizes of the black bodies"?
Yes, they certainly mean “nonzero.” In physics, “nonzero” has become an accepted meaning of “finite,” I’m sorry to say.
I’ve just thought about this for a couple of minutes and haven’t looked anywhere else so, with that caveat, here’s my take: Yes, some photons from B will hit the sphere and bounce back to B. This is equivalent to the photon never having left B in the first place. When it gets re-emitted, so to speak, it might hit the ellipsoid next time. So, just as many get from A to B as from B to A.
You should mention what (b) is for.
You’re right — I should comment on (b). It’s an alternative version of essentially the same puzzle. It’s not really necessary to have both, and if I had been ever so slightly less lazy, I would have cut it out to avoid distraction.
Since I didn’t, I’ll describe the setup in (b). This time, you have parts of just one ellipsoid and one sphere centered on B. This situation still leads to a net flow of energy from A to B, but in a more complicated way. All photons from B go either to A (by hitting the ellipsoid) or to B (by hitting the sphere). Some photons from A hit the ellipsoid and make it to B; some hit the sphere and it’s not totally clear what happens to them. (They bounce around many times, for sure. They can’t end up at B, because if they did then by reversing their trajectory we can see that they must have come straight from A by way of the ellipsoid, which we know is not the case. Do they eventually make it back to A or bounce around forever? I don’t know.)
No matter what happens to those photons that went from A to the sphere, it follows that B heats up (assuming we started with identical equal-temperature sources at A and B): since the solid angle of the ellipsoid as seen from A is greater than the solid angle as seen from B, the number of A photons reaching B is greater than the number of B photons being “lost” to A.