I know: as headlines go, this one is not exactly Man Bites Dog. Let me be a bit more specific. Either the New York Times or trial lawyers don’t understand probability. (This, incidentally, is a good example of the inclusive “or”.)
The Times has an interactive feature illustrating the process by which lawyers decide whether to allow someone to be seated on a jury. For those who don’t know, in most if not all US courts, lawyers are allowed to have potential jurors stricken from jury pools, either for cause, if there’s evidence that a juror is biased, or using a limited number of “peremptory challenges” to remove people that the lawyer merely suspects will be unfavorable to his or her side. The Times piece asks you a series of questions and indicates how your answers affect the lawyers’ opinion about you in a hypothetical lawsuit by an investor suing her money manager for mismanaging her investments.
The first two questions are about your job and age. As a white-collar worker, I’m told that I’d be more likely to side with the defendant, but the fact that I’m over 30 makes me more likely to favor the plaintiff. A slider at the top of the screen indicates the net effect:
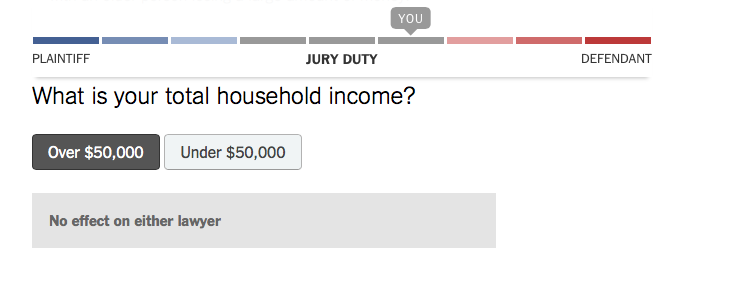
So far so good. Question 3 then asks about my income. Here are the two possible outcomes:
So if I’m high-income, there’s no effect, but if I’m low-income, I’m more likely to side with the plaintiff. This is logically impossible. If one answer shifts the probability one direction, the other answer must shift it the other direction (by some nonzero amount).
Before the lawyers found out the answer, they knew that I was either low-income or high-income. (A waggish mathematician might observe that the possibility that my income is exactly $50,000 is not included in the two possibilities. This is why no one likes a waggish mathematician.) The lawyers’ assessment of me before asking the question must be a weighted average of the two subsequent possibilities, with weights given by their prior beliefs about what my income would turn out to be. For instance, if they thought initially that there was a 70% chance that I’d be in the high-income category, then the initial probability should have been 0.7 times the high-income probability plus 0.3 times the low-income probability.
That means that if one answer to the income question shifts the probability toward the plaintiffs, then the other answer must shift the probability in the other direction.
So either the lawyers the reporter talked to are irrational or the reporter has misunderstood them. For what it’s worth, my money is on the first option. Lots of people don’t understand probabilities, but it seems likely to me that the Times reporters would have asked these questions straightforwardly and accurately reported the answers they heard from the lawyers they talked to.
If that’s true, it seems like it should present a money-making opportunity for people with expertise in probability. Lawyers who hired such people as consultants would presumably do a better job at jury selection and win more cases.


Of course, a) having just a rich/poor choice, b) setting this (probably arbitrarily) at $50,000, and asking about only income but not net worth makes such a scheme very coarse, even if it were implemented correctly.
By the way, does this have anything to do with Mr. T recently having been de-selected for jury duty?
There are other serious problems with lawyers not understanding probability, such as the prosecutor’s fallacy.
I’m going to guess that these results are based on logistic regression with “probability of voting in favor of the plaintiff” as the dependent variable. The explanatory variables, corresponding to the questions in the survey, are all categorical, so for each question one of the responses is treated as a sort of default and the parameters for the other responses are (log) odds ratios relative to the default.
So I think the error here is in the way the questions are phrased. It would be more precise to say something like: “The initial estimate is based on the assumption that you are employed and make more than $50K (and so on for the other questions). If you tell me different, I will update my beliefs accordingly. But if you confirm my assumption, that has no effect.”
So that’s my attempt to give everyone involved the benefit of the doubt. However, there is another oddity you didn’t mention, Ted. The text suggests that lawyers are updating probabilities differently depending on whether they represent the plaintiff or the defendant.
The only way I can make _that_ rational is if lawyers make different modeling assumptions, depending on who they represent, and therefore compute different odds ratios. And I suppose their modeling choices could be justified by different costs for different kinds of errors.
I was going to say it didn’t seem that simple to me, but I think Allen just did that far better than I could.
From a naive perspective, the result they show is cumulative, some sort of weighted sum of the answers so far. The questions aren’t independent, and some answers are far more determinative than others, so looked at that way the weights must be dependent on the answers. But that’s probably not the best way to look at it. Kind of like the latest vaccine kerfuffle, where the original analysis used conditional logistic regression, and the (incorrect) reanalysis used a naive Pearson’s chi-squared that takes no account of confounders.
wrt different modeling assumptions, one place different costs of errors might be introduced is in how likely a juror is to influence other jurors.
Also, one picky point–I believe the NYT talked to jury selection consultants, who often are social scientists or other specialties, not lawyers. So, whatever your prior is about lawyers not understanding statistics should have limited weight over jury selection specialists.
I love it. I’ve just added a new goal to my list. Within, say the next year, I must take any opportunity to say “This is why no one likes a waggish mathematician.”
Oops… a typo. That last sentence suffers from an erroneous comma – a mistake for which I have a new favorite example (as of a few days ago)
Let’s eat, Grandma!
vs.
Let’s eat Grandma!
“I dedicate this thesis to my parents, God and L. Ron Hubbard” demonstrates that the “when in doubt, leave it out” rule for commas is often not correct.
I used to always leave out the comma before the “and” in a list of three or more items, by analogy with the two-item case. I now include it, since one usually pauses before the “and” in a longer list where one doesn’t in a two-item list. (Sort of like James Joyce, whose punctuation often reflects the length of a pause more than anything else.)