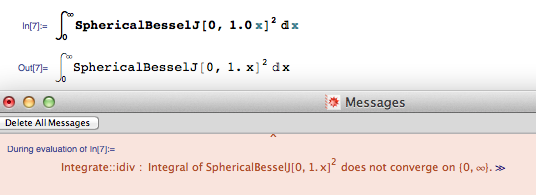
So far so good. This is the correct result. Now multiply the x by 1.0:
That makes Mathematica think that the integral fails to converge.
I found this out when reproducing some calculations from a couple of years ago. It seemed to work back then, so this behavior seems to have been introduced in a recent version of Mathematica.
I know of various reasons why putting in the 1.0 could make a difference (because it forces Mathematica to think in terms of floating-point numbers with finite accuracy, rather than exact integers), but I don’t think any of them should make a difference here. The integral is failing to converge at x=0 (I checked that the problem is there, not at infinity), and the integrand is perfectly well-behaved there, even if you replace the 1.0 by any other complex number.