My friend Allen Downey posted a model of how the falling slinky behaves, with the goal of calculating how the top end moves. (In my post, I focused just on the fact that the bottom end stays still for so long.) Allen’s approach is clever and gets some of the large-scale features right but is wrong in detail (as he agrees). Let me see if I can fix it up a bit.
Allen observes that the slinky seems to completely collapse from the top down. That is, at any given moment, there’s a point above which the slinky is completely collapsed and below which it’s the same as it was originally. He uses that, along with the fact that the center of mass has to descend in the usual constant-acceleration way, to work out the rate at which the top end has to move. The problem is that the analysis assumes the slinky has uniform density, which isn’t true: it’s much more stretched out at the top than at the bottom.
Warning: equations and integrals ahead. Skip to the graphs near the end if you want.
To fix this up, we need to know how the density varies along the slinky’s length. I claim that, to a pretty good approximation, the initial density is proportional to 1/sqrt(y), where y is the height measured up from the bottom of the slinky. Here’s why.
Consider a small piece of the slinky at height y, with width dy. If L(y) is the linear mass density, then the mass of this piece is L(y) dy, and the force of gravity on it is g L dy. Initially, this piece is at rest, so this force must be balanced by the spring tension on either side of it. The tension in the spring is proportional to 1/L (the more the spring is stretched, the smaller the mass density). The upward forces by the pieces right above and below the segment in question are proportional to [1/L(y+dy)] and 1/L(y) respectively. Since they pull in opposite directions, the net force is the difference between these two, which is dy times the derivative of 1/L. So
(1/L)’ = constant times L.
The solution to this is L proportional to 1/sqrt(y+constant). We want the tension in the spring to be essentially zero at the bottom, so the constant inside the square root is zero. (This approximation breaks down somewhere very near the bottom, but I’m not too worried about that.)
For convenience, I’ll choose my unit of length so that the initial length of the slinky is 1 and my unit of mass so that the constant of proportionality in the density is 1:
L(y) = y-1/2, for 0<y<1.
As you can check by doing a couple of integrals, in these units, the total mass of the slinky is 2, and the center of mass is initially 1/3 of the way up.
Now adopt Allen’s model. At any given time t, there is some Y(t) such that the part of the slinky above Y has completely collapsed and the part below hasn’t moved at all. We’ll assume that the collapsed part can be modeled as having zero height, so that all that stuff is at the height Y. Then the position of the center of mass is
We know that the center of mass must drop according to the usual free-fall rule,
ycm = 1/3 – (1/2) gt2.
Having already chosen weird units of length and mass, we might as well choose units of time so that g = 1.
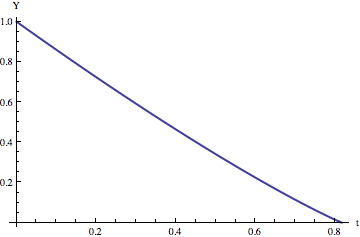
Now we set those two expressions for the center of mass equal and solve for Y. Sadly, the resulting equation is a cubic. Cardano and Mathematica know how to solve it, but the solution is a very complicated and unenlightening formula. Here’s a graph of it, though.
For those who skipped over the equations and are just joining us, this is, according to my model, the position of the topmost point on the slinky as a function of time.
Here’s the interesting thing: this graph looks really really close to a straight line. That is, the top of the spring moves at roughly constant velocity. Allen’s original argument led to the conclusion that it moves at exactly constant velocity, which turns out to be not that far wrong.
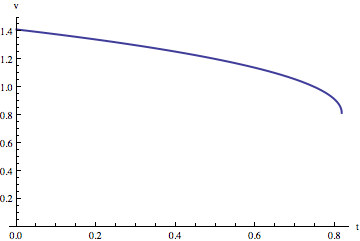
Here’s a graph showing the velocity of the topmpost point on the slinky as a function of time:
The top end actually slows down a bit, according to this model.
We offer a computational methods class from time to time in our department. It’d be a nice assignment to model this system numerically in detail and compare the results both with the above model and with video-captured data from a real falling slinky.
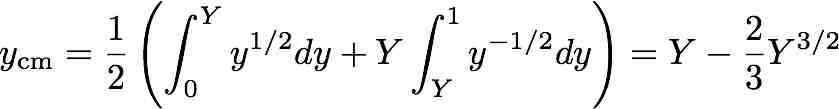
Nice calculations!
I wish in the video they’d dropped a ball from the height of the top of the slinky so that you could track things. Or, maybe even better, dropped a ball from the height of the CM of the slinky, but that would be harder to calculate and to synchronize with the release of the top of the slinky.
How does the top end slow down? I can’t find a breaking (upward) force on it.
As the fully-collapsed bit at the top falls, it keeps crashing into more parts of the slinky that are still at rest. Each such collision gives an upward impulse to the collapsed bit.
To put it another way, the mass of the fully-collapsed bit keeps going up, so even if its momentum didn’t change at all, it’d slow down.
Pretty accurate calculation!