In a discussion of David Hogg’s and my quixotic quest to convince people that it’s OK to think of the redshifts of distant galaxies as being due to the galaxies’ motion (that is, as a Doppler shift), Phillip Helbig writes
I think we all must agree on the following statement: Using the relativistic Doppler formula to calculate the velocity of an object at high redshift does not yield a meaningful answer in the the velocity so derived is not the temporal derivative of ANY distance used for other purposes in cosmology.
I replied to him in the comments, but I think that this point needs a longer response and might be of more general interest.
I agree with the beginning and end of Phillip’s statement, but not the middle. To be precise, I agree that the velocity derived from the Doppler formula is not the derivative of a distance, but I don’t agree that that means it’s not a meaningful velocity.
That’s right: I’m saying a velocity is not necessarily the rate of change of a distance. That sounds crazy: isn’t that the definition of velocity?
Well, sometimes. But there are other times in astrophysics when a Doppler shift is measured, and nobody objects to calling the resulting quantity a velocity, even though that quantity is not the rate of change of a distance (or more generally of a position). The clearest example I know of is a binary star.
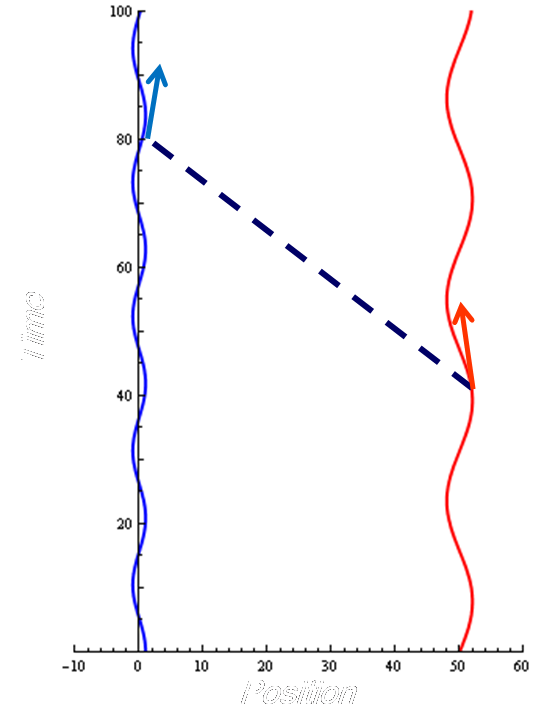
Here’s a cartoon spacetime diagram of an observation of a binary star.
Time increases upward on this diagram. The blue curve represents the Earth. The curve wobbles back and forth as the Earth orbits the Sun. The red curve represents a star, which is orbiting another star (not shown). The dashed curve shows the path of a photon going from the star to the observer.
This is a situation that occurs all the time in astronomy. The observer sees the photon (many photons, actually), measures a redshift, and calls the result the velocity of the star relative to us.
Now riddle me this: What is the position function x(t) such that this velocity is dx/dt? For that matter, at what t should this derivative be evaluated?
There is no good answer to this question. The velocity in question is not equal to the time derivative of a position, in any useful sense. The main reason is that the velocity in question is a relative velocity, relating motion at two different times.
If you insist on describing the measured velocity of the star as a dx/dt, here’s the best way I can think of to do it. Define an inertial reference frame in which the Earth is at rest at the moment of observation. Then the measured velocity is dx/dt, where (x,t) are the coordinates of the star in this frame, and the derivative is evaluated at the time of emission. But this doesn’t meet Phillip’s criterion: the quantity x in this expression is not a “distance used for any other purpose.” It’s certainly not in any sense the distance from the Earth to the star, for instance: at the time the derivative is evaluated, the Earth was nowhere near the right location for this to be true.
The velocity of the Earth, in some chosen reference frame, is a dx/dt, and the velocity of the star is also a dx/dt. (Each of these two is represented by an arrow in the picture above.) But the relative velocity of the two isn’t. If you’re unwilling to call this quantity a velocity, then I guess you should be unwilling to call the quantity derived from a cosmological redshift a velocity. But this seems to me a bit of a Humpty Dumpty way to talk.
I think the way you define things is correct in principle, but too exact in practice. It’s like saying we don’t know anything except what we experience directly (if that) because, according to statistical mechanics, a kettle of water on a stove can freeze (it’s just very improbable), any “stable” nucleus can spontaneously tunnel to iron-56 (it’s just very improbable) etc. So we can’t know what will happen tomorrow even though we think we can extrapolate well from the present, according to the laws of physics. It’s almost as bad as Frank Tipler’s latest book. 🙂 I would argue that, in the example of the binary star, in the limit of small cosmological distance (true in practice), the velocity measured is the derivative of practically any distance (since various distances are degenerate in this case). During an election campaign, each candidate should prefix all campaign promises with “assuming I am elected and otherwise have a majority to support me”. It’s so trivial that everyone knows it is true, so it is left out in the interest of brevity and confuses no-one in practice.
I’m sorry, but I’m completely baffled by your “derivative of practically any distance” comment. I’m not talking about tiny effects, and I’m not talking about weird relativistic effects. Even in good old Newtonian physics, I honestly can’t think of any sensible notion of distance such that the measured velocity is even close to dx/dt.
Give me a hint here: At which value of t are you imagining evaluating dx/dt? Emission or observation?
To be definite, suppose that the star is 10.5 light-years away from the Earth, and that the period of the star’s orbit is 7.25 years. Note that if you choose emission, then the Earth’s velocity at that time will not match the value that goes into the measurement. Similarly, if you choose absorption, the star’s velocity won’t match.
I think we’re talking past each other. If we ever meet (perhaps at the next Texas Symposium?) perhaps we can have a face-to-face discussion.
I suspect the answer is the combination of the velocity at emission and the velocity at reception, sort of like the situation you describe in the cosmological case.
The cyclical example of a binary star complicates things but is, I think, a red herring. Think of a star with a peculiar motion along the line of sight.
You seem to be saying that the whole idea of 3-D astrometry (Hipparcos, Gaia etc) doesn’t make any sense.
I certainly don’t believe, nor did I say, anything like the last sentence.
Let’s recap.
You objected to my interpretation of the cosmological redshift, because the velocity involved “is not the derivative of a distance used in other contexts” or something like that. I presented an example from good old Newtonian (not even special-relativistic) astronomy in which a velocity is measured that is not such a derivative. It follows that “derivative of a distance” is not a required criterion to call something a velocity.
You disagreed with that statement but cannot supply me with a function x(t), or a value of t for that matter, such that the velocity in question is dx/dt.
Let’s be incredibly specific. The proper distance between the Earth and the binary star is of the form
x(t) = d + a1 cos(w1 t+phi1) + a2 cos(w2 t+phi2).
The measured velocity is not dx/dt, whether t is the time of emission, observation, or “some combination” of the two.
I hope we at least agree that the discussion is mainly about terminology.
“It follows that "derivative of a distance" is not a required criterion to call something a velocity.” If I’m willing to accept that, both for the binary star and for the cosmological redshift, don’t you agree that describing the cosmological redshift as a Doppler shift is confusing because most people think of the Doppler shift as measuring a “conventional” velocity? On the other hand, if one starts out by showing how a velocity doesn’t have to be the temporal derivative of a distance, then much of the confusion about the applicability of the Doppler shift in the cosmological case goes away.
With regard to astrometry: positions and velocities (parallel and perpendicular to the line of sight) are measured and used to predict and retrodict the positions of stars at various times in the past and future, say in the galactic reference frame, even though all these measured velocities suffer the same problem as in the binary-star case. This doesn’t seem to be a problem for astrometry.
Except in the limit of zero distance, can a redshift be used to deduce any sort of conventional velocity (temporal derivative of a distance) in any situation?
I certainly agree with the first sentence. I’ve tried to be extremely clear all along that I’m not saying anything nonstandard about the physics — the only question is which words to wrap around the physics.
The second paragraph utterly baffles me. Do you think it’s “confusing” to describe the redshift of the binary star as a Doppler shift? If so, then I think you’re in a tiny minority. If not, then why is it “confusing” to use the same words to describe the precisely analogous case of the cosmological redshift?
Personally, I’m completely comfortable with the idea that the star’s measured velocity is a velocity, even though it’s not a dx/dt. That’s a slightly curious but ultimately perfectly acceptable consequence of the fact that we’re comparing events at two different times. And again, every part of that statement applies just as well to the cosmological redshift.
I still don’t get the problem with astrometry. If someone were to think that a velocity measured via a Doppler shift was a dx/dt at a fixed time, then that person would be making a mistake, which might or might not be significant depending on the time scales. I have no reason to think that anyone who does astrometry is making such a mistake, though.
To answer the last question: in the limit where the light-travel time is small compared to other relevant time scales (particularly the time scales on which velocity changes), the velocity associated with the observed redshift approaches what you’re calling a “conventional velocity.” In both the binary star case and the cosmological case, we’re not in that limit. In the former case, it seems absurd to suggest that we shouldn’t call the observed shift a Doppler shift. Therefore the “v is not dx/dt” argument is not a valid argument against calling something a Doppler shift. That’s all I’m saying.
“Personally, I'm completely comfortable with the idea that the star's measured velocity is a velocity, even though it's not a dx/dt.”
“Therefore the "v is not dx/dt" argument is not a valid argument against calling something a Doppler shift. That's all I'm saying.”
I think this is the essence of the argument. To me (and maybe to other people), the idea that v is defined as dx/dt seems obvious. I suspect that this was Harrison’s motivation as well for supporting the “expanding space” paradigm. This usually unstated assumption is probably the cause of most of the confusion on this subject.
OK. I assume then, that when you next talk to an astronomer who studies binary stars or extrasolar planets, you will carefully explain to them that what they are measuring are not Doppler shifts or velocities. Let me know how that works out.
Actually I was agreeing with you. 😐
Oh. Sorry!