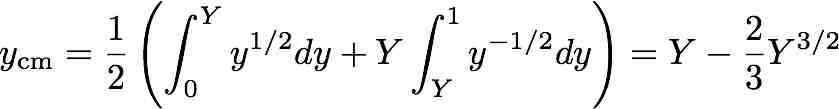Ted Bunn’s Blog

I’m pleased to report that the University of Richmond physics department has an opening for a tenure-track faculty member. Research specialty is wide open. Here’s the text of the job ad, which will be going out on Physics Today soon.

If you’re looking for a faculty job at a place where both teaching and research are valued, UR is a great place to work. Please pass the word about this position on to anyone you think would be interested.

 

Faculty Position in Physics

The Department of Physics at the University of Richmond invites applications for a tenure-track faculty position as an assistant professor in physics to begin in August 2013 (for exceptional candidates an appointment at a more senior level might be considered). Applications are encouraged from candidates in all sub-fields of physics, both theory and experiment, but applications from candidates whose scholarship complements existing research areas in the department (biophysics, cosmology, low- and medium-energy nuclear physics and surface physics) may receive particular attention. The successful candidate is expected to have demonstrated a keen interest and ability in undergraduate teaching and to maintain a vigorous research program that engages undergraduates in substantive research outcomes. Candidates must possess a doctoral degree in physics prior to appointment.

Candidates should apply online at the University of Richmond Online Employment website (https://www.urjobs.org) using the Faculty (Instructional/Research) link. Applicants are asked to submit a cover letter, a current curriculum vitae with a list of publications, a statement of their teaching interests and philosophy, evidence of teaching effectiveness (if available), a description of current and planned research programs, and the names of three references who will receive an automated email asking them to submit their reference letters to this web site. Review of applications will commence November 1, 2012 and continue until the position is filled.

The University of Richmond is a highly selective private university with approximately 3000 undergraduates located on a beautiful campus six miles west of the heart of Richmond and in close proximity to the ocean, mountains, and Washington D.C. The University of Richmond is committed to developing a diverse workforce and student body and to being an inclusive campus community. We strongly encourage applications from candidates who will contribute to these goals. For more information please see the department’s website at http://physics.richmond.edu or contact Prof. C.W. Beausang, Chair, Department of Physics, (email: cbeausan@richmond.edu).

My last post reminded me of another post by Peter Coles that I meant to link to. This one’s about journal impact factors. For those who don’t know, the impact factor is a statistic meant to assess the quality or importance of a scholarly journal. It’s essentially the average number of citations garnered by each article published in that journal.

It’s not clear whether impact factors are a good way of evaluating the quality of journals. The most convincing argument against them is that citation counts are dominated by a very small number of articles, so the mean is not a very robust measure of “typical” quality. But even if the impact factor is a good measure of journal quality, it’s clearly not a good measure of the quality of any given article. Who cares how many citations the other articles published along with my article got? What matters is how my article did. Or as Peter put it,

The idea is that if you publish a paper in a journal with a large [journal impact factor] then it’s in among a number of papers that are highly cited and therefore presumably high quality. Using a form of Proof by Association, your paper must therefore be excellent too, hanging around with tall people being a tried-and-tested way of becoming tall.

But people often do use impact factors in precisely this way. I did it myself when I came up for tenure: I included information about the impact factors of the various journals I had published in in order to convince my evaluators that my work was important. (I also included information about how often my own work had been cited, which is clearly more relevant.)

Peter’s post is based on another blog post by Steven Curry, which ends with a rousing peroration:

• If you include journal impact factors in the list of publications in your cv, you are statistically illiterate.
• If you are judging grant or promotion applications and find yourself scanning the applicant’s publications, checking off the impact factors, you are statistically illiterate.
• If you publish a journal that trumpets its impact factor in adverts or emails, you are statistically illiterate. (If you trumpet that impact factor to three decimal places, there is little hope for you.)
• If you see someone else using impact factors and make no attempt at correction, you connive at statistical illiteracy.

I referred to impact factors in my tenure portfolio despite knowing that the information was of dubious relevance, because I thought that it would impress some of my evaluators (and even that they might think I was hiding something if I didn’t mention them). Under the circumstances, I plead innocent to statistical illiteracy  but nolo contendere to a small degree of cynicism.

To play devil’s advocate, here is the best argument I can think of for using impact factors to judge individual articles: If an article was published quite recently, it’s too soon to count citations for that article. In that case, the journal impact factor provides a way of predicting the impact of that article.

The problem with this is that the impact factor is an incredibly noisy predictor, since there’s a huge variation in citation rates for articles even within a single journal (let alone across journals and disciplines). If you’re on a tenure and promotion committee, and you’re holding the future of someone’s career in your hands, it would be outrageously irresponsible to base your decision on such weak evidence. If you as an evaluator don’t have better ways of judging the quality of a piece of work, you’d damn well better find a way.

Peter Coles has a nice post on Thomas Kuhn’s place in the philosophy of science. Many people seem to regard Kuhn’s book The Structure of Scientific Revolutions as, well, revolutionary in its effect on how we think about the nature of scientific progress and its relation to objective truth.

I confess that I never really got the point of Structure of Scientific Revolutions, so I’m glad to see that Peter’s on the same page. He goes further than I’d ever thought of going, placing Kuhn on a continuum leading from Hume and Popper through to the clownish yet pernicious writings of Feyerabend. I’m not sure I’d go so far as to hang Feyerabend around Kuhn’s neck, but maybe Peter’s right.

Anyway, in addition to putting down Kuhn et al.’s vision of what science is, Peter advances his own view, which is 100% right, in my opinion. I tried to say much the same thing in my own way a few years ago, but Peter’s version is probably better.

that’s anywhere near as good as this.

 

 

The news these days is filled with polarization, with hate, with fear, with ignorance. But while these feelings are a part of us, and always will be, they neither dominate nor define us. Not if we don’t let them. When we reach, when we explore, when we’re curious – that’s when we’re at our best. We can learn about the world around us, the Universe around us. It doesn’t divide us, or separate us, or create artificial and wholly made-up barriers between us. As we saw on Twitter, at New York Times Square where hundreds of people watched the landing live, and all over the world: science and exploration bind us together. Science makes the world a better place, and it makes us better people.

This definitely increases the awesome.

 

A political scientist named Andrew Hacker had an opinion piece in this past Sunday’s New York Times headlined “Is Algebra Necessary?” It begins

A typical American school day finds some six million high school students and two million college freshmen struggling with algebra. In both high school and college, all too many students are expected to fail. Why do we subject American students to this ordeal? I’ve found myself moving toward the strong view that we shouldn’t.

I guess no one who knows me will be too shocked to hear that I disagree.

Before going any further, let me stipulate something. I am not claiming that our math curriculum is perfect as it is. I suspect that certain changes, particularly an increased emphasis on mathematical intuition and data literacy at the expense of more abstract topics, might be a good idea. In fact, if Hacker had taken aim at calculus instead of algebra, I might be largely with him. Many college-bound students who get sent off on the death march towards calculus would be better off truly mastering more basic ideas instead. But algebra’s the wrong target for his ire.

Here’s the simple, obvious point. If you don’t teach algebra in high school, you are closing huge numbers of doors into careers in the STEM fields (that’s science, technology, engineering, and mathematics). Hacker disputes this with an anecdote about Toyota partnering with a community college to teach employees “machine tool mathematics” to indicate that it’s OK if high schools don’t teach these skills. Count me unconvinced.

STEM covers a bunch of different things, but let’s focus on just the E part. If you haven’t learned algebra (at least) in high school, you will not be an engineer. Period. (I urge Hacker to walk over to the pre-engineering program at his university and ask the folks there.) If you take algebra out of the standard high school curriculum, you will not train American engineers. Needless to say, high school students in the rest of the world will not unilaterally disarm and stop learning algebra because we do. Our teenagers will simply not be able to compete.

The same goes for a bunch of jobs in the S and T parts of STEM, and of course all of the M part. For instance, any job that involves understanding how a computer program works — not just software engineers but pretty much anything peripherally related to the field — requires understanding the ideas of variables and functions, otherwise known as algebra.

Hacker says

It would be far better to reduce, not expand, the mathematics we ask young people to imbibe. (That said, I do not advocate vocational tracks for students considered, almost always unfairly, as less studious.)

That parenthetical comment at the end is extremely ironic. The result of the changes he proposes would be tracking on a massive scale, in which only the small minority of students whose parents have the wherewithal to put them into special programs or private schools are eligible for many of the best jobs.

Hacker suggests that we should be teaching courses in things like “citizen statistics,” which “familiarize students with the kinds of numbers that describe and delineate our personal and public lives.” For example, such a course

could, for example, teach students how the Consumer Price Index is computed, what is included and how each item in the index is weighted — and include discussion about which items should be included and what weights they should be given.

I’m 100% for this. But here’s the thing. Understanding even the idea of a weighted average involves (basic) algebra.

By all means, let’s teach algebra and related subjects in ways that relate to important topics. Let’s emphasize why the tools in these courses are important, even if that means de-emphasizing some of the more formal and abstract aspects of the subject. To steal one of Hacker’s examples, I’m OK if not all students become proficient at factoring polynomials. If we swap that out in favor of improving skills at reading and interpreting graphs, for instance, that’d be fine. But the main ideas of algebra — particularly the idea that you can figure things out about variables in general, rather than having to work out each case one at a time, and the idea of a function — are essential for all kinds of basic quantitative reasoning.

A couple of little final notes.

In his concluding paragraph Hacker says

Yes, young people should learn to read and write and do long division, whether they want to or not.

Actually, long division would be pretty high up on my list of things that could be jettisoned. We don’t teach people to do “long square roots” (yes, there is an algorithm for computing square roots by hand). Long division is only marginally more useful.

Then there’s medicine. Hacker notes

Medical schools like Harvard and Johns Hopkins demand calculus of all their applicants, even if it doesn’t figure in the clinical curriculum, let alone in subsequent practice.  Mathematics is used as a hoop, a badge, a totem to impress outsiders and elevate a profession’s status.

It’s true that calculus isn’t really necessary for doctors (and neither, truth be told, is most of the physics they’re supposed to learn). I think the reason that stuff is in the pre-med curriculum is partly a status thing as he suggests, but also just a general test of intelligence and ability to learn difficult things. To be honest, I’d be worried about being treated by a doctor who didn’t have the ability and perseverance to learn basic calculus, even though they don’t actually need to use calculus to treat me. But if you replaced calculus by something equally challenging, I’d be OK with that.

No doubt anyone who’s reading this already knows about the web comic xkcd. (If not, drop what you’re doing and start reading it.) But you may not know that the author, Randall Munroe, has started a new feature in which he answers a weekly “what if” question about physics (broadly construed). There have been three entries so far:

• What would happen if you tried to hit a baseball pitched at 90% of the speed of light?
• What if everyone who took the SAT guessed on every multiple-choice question? How many perfect scores would there be?
• How much Force power can Yoda output?

I actually don’t think his answer to the first one is quite right. He says there’d be a lot of nuclear fusion reactions, but I don’t see any reason to think there would be. The collisions are certainly energetic enough for fusion to happen, but I think the probabilities (cross sections) for other reactions, mostly simple scattering, are much higher than for fusion. At first I thought that this made a big qualitative difference in the expected behavior, but I don’t actually think it does: the ball’s kinetic energy is so large that the extra energy released via fusion wouldn’t make much difference anyway.

Anyway, that’s a quibble. The main point is to entertain (while conveying some scientific information), and as you’d expect Munroe is awesome at that. A little excerpt:

Next, we need to know how fast it was rising. I went over footage of the scene and timed the X-Wing’s rate of ascent as it was emerging from the water.

 

The front landing strut rises out of the water in about three and a half seconds, and I estimated the strut to be 1.4 meters long (based on a scene in A New Hope where a crew member squeezes past it), which tells us the X-Wing was rising at 0.39 m/s.

Lastly, we need to know the strength of gravity on Dagobah. Here, I figure I’m stuck, because while sci-fi fans are obsessive, it’s not like there’s gonna be a catalog of minor geophysical characteristics for every planet visited in Star Wars. Right?

Nope. I’ve underestimated the fandom. Wookieepeedia has just such a catalog, and informs us that the surface gravity on Dagobah is 0.9g.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

My friend Allen Downey posted a model of how the falling slinky behaves, with the goal of calculating how the top end moves. (In my post, I focused just on the fact that the bottom end stays still for so long.) Allen’s approach is clever and gets some of the large-scale features right but is wrong in detail (as he agrees). Let me see if I can fix it up a bit.

Allen observes that the slinky seems to completely collapse from the top down. That is, at any given moment, there’s a point above which the slinky is completely collapsed and below which it’s the same as it was originally. He uses that, along with the fact that the center of mass has to descend in the usual constant-acceleration way, to work out the rate at which the top end has to move. The problem is that the analysis assumes the slinky has uniform density, which isn’t true: it’s much more stretched out at the top than at the bottom.

Warning: equations and integrals ahead. Skip to the graphs near the end if you want.

To fix this up, we need to know how the density varies along the slinky’s length. I claim that, to a pretty good approximation, the initial density is proportional to 1/sqrt(y), where y is the height measured up from the bottom of the slinky. Here’s why.

Consider a small piece of the slinky at height y, with width dy. If L(y) is the linear mass density, then the mass of this piece is L(y) dy, and the force of gravity on it is g L dy. Initially, this piece is at rest, so this force must be balanced by the spring tension on either side of it. The tension in the spring is proportional to 1/L (the more the spring is stretched, the smaller the mass density). The upward forces by the pieces right above and below the segment in question are proportional to [1/L(y+dy)] and 1/L(y) respectively. Since they pull in opposite directions, the net force is the difference between these two, which is dy times the derivative of 1/L. So

(1/L)’ = constant times L.

The solution to this is L  proportional to 1/sqrt(y+constant). We want the tension in the spring to be essentially zero at the bottom, so the constant inside the square root is zero. (This approximation breaks down somewhere very near the bottom, but I’m not too worried about that.)

For convenience, I’ll choose my unit of length so that the initial length of the slinky is 1 and my unit of mass so that the constant of proportionality in the density is 1:

L(y) = y^-1/2, for 0<y<1.

As you can check by doing a couple of integrals, in these units, the total mass of the slinky is 2, and the center of mass is initially 1/3 of the way up.

Now adopt Allen’s model. At any given time t, there is some Y(t) such that the part of the slinky above Y has completely collapsed and the part below hasn’t moved at all. We’ll assume that the collapsed part can be modeled as having zero height, so that all that stuff is at the height Y. Then the  position of the center of mass is

We know that the center of mass must drop according to the usual free-fall rule,

y_cm = 1/3 – (1/2) gt².

Having already chosen weird units of length and mass, we might as well choose units of time so that g = 1.

Now we set those two expressions for the center of mass equal and solve for Y. Sadly, the resulting equation is a cubic. Cardano and Mathematica know how to solve it, but the solution is a very complicated and unenlightening formula. Here’s a graph of it, though.

For those who skipped over the equations and are just joining us, this is, according to my model, the position of the topmost point on the slinky as a function of time.

Here’s the interesting thing: this graph looks really really close to a straight line. That is, the top of the spring moves at roughly constant velocity. Allen’s original argument led to the conclusion that it moves at exactly constant velocity, which turns out to be not that far wrong.

Here’s a graph showing the velocity of the topmpost point on the slinky as a function of time:

The top end actually slows down a bit, according to this model.

We offer a computational methods class from time to time in our department. It’d be a nice assignment to model this system numerically in detail and compare the results both with the above model and with video-captured data from a real falling slinky.

 

Check out this video of a falling slinky:

[Update: Video was wrong for a while. I think it should be right now.]

The person who made this, who seems to go by the name Veritasium, has some other sciency-looking videos on his YouTube channel, by the way. I haven’t checked out the others.

In principle, it should be obvious to a physicist that the bottom of a hanging slinky can’t start to move for quite a while after the top end is dropped. To be specific, the information that the top end has been dropped can’t propagate down the slinky any faster than the speed of sound in the slinky (i.e., the speed at which waves propagate down it), so there’s a delay before the bottom end “knows” it’s been dropped. But it’s surprising (at least to me) to see how long the delay is.

There are a couple of different ways to explain this. One is essentially what I just said: the bottom of the slinky doesn’t know to start falling because the information takes time to get there. The other is

[T]he best thing is to think of the slinky as a system. When it is let [go], the center of mass certainly accelerates downward (like any falling object). However, at the same time, the slinky (spring) is compressing to its relaxed length. This means that top and bottom are accelerating towards the center of mass of the slinky at the same time the center of mass is accelerating downward.

These are both right. Personally, I think the information-propagation explanation is a nicer way to understand the most striking qualitative feature of the motion (that the bottom stays put for so long). But if you wanted to model the motion in detail you’d want to write down equations for all the forces.

Anyway, it’s a nice illustration of a very common occurrence in physics:  you can give two explanations of a phenomenon that sound extremely different but are secretly equivalent.

(I saw this on Andrew Sullivan’s blog, in case you were wondering.)

Interesting report from Nature about the teaching of evolution (or rather the lack of it) in South Korea.

Mention creationism, and many scientists think of the United States, where efforts to limit the teaching of evolution have made headway in a couple of states1. But the successes are modest compared with those in South Korea, where the anti-evolution sentiment seems to be winning its battle with mainstream science.

A petition to remove references to evolution from high-school textbooks claimed victory last month after the Ministry of Education, Science and Technology (MEST) revealed that many of the publishers would produce revised editions that exclude examples of the evolution of the horse or of avian ancestor Archaeopteryx. The move has alarmed biologists, who say that they were not consulted.

One interesting contrast between US and Korean creationism:

However, a survey of trainee teachers in the country concluded that religious belief was not a strong determinant of their acceptance of evolution.

It’s not totally clear to me what the reason is if not religious belief.

Another interesting nugget:

It also found that 40% of biology teachers agreed with the statement that “much of the scientific community doubts if evolution occurs”; and half disagreed that “modern humans are the product of evolutionary processes”.

I’ve always imagined that relatively few biology teachers are actual creationists: I imagine that they actually know that there’s a complete scientific consensus that evolution is right, even if they don’t teach it in class as much as they should (often due to external pressures). But according to this, lots of South Korean biology teachers are sincere creationists. It started me wondering whether the same is true in the US.

Here’s a survey of US biology teachers that addresses the question. Almost all of the survey has to do with what teachers teach in class (and is very interesting). As far as I can tell, there’s just one question that’s about what the teachers actually believe:

The questions are different, so it’s hard to do a head-to-head comparison between the US and South Korean teachers. Clearly everyone in the last group would disagree with the  statement that “modern humans are the product of evolutionary processes,” and everyone in the second group would agree with it, but what about the majority in the first group? I suspect that many of them would agree with the statement, but it’s hard to know for sure.

This is a depressing subject for most scientists, so here’s one little ray of sunshine from the survey:

Or does the fact that I’m encouraged to see that “only” 13% of science teachers believe this simply show how depressingly low my expectations are?

Anyway, if you’re interested in this stuff, it’s worth browsing around the rest of the survey results.