Mother Jones has a writeup of a very interesting psychology study on how political views affect people’s ability to draw mathematical conclusions.
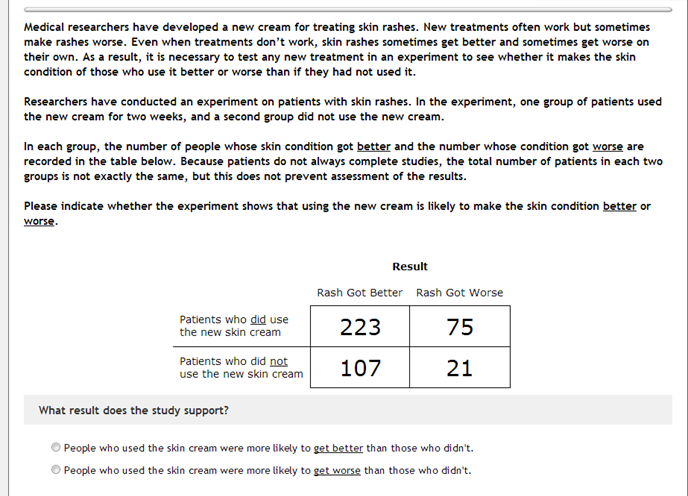
A group of psychologists gave a bunch of people a math problem:
Lots of people get this wrong. (That’s not the surprising part.)
Here’s where things get more interesting. They changed the problem into one about gun control: leaving the numbers exactly the same, they posed the problem as one about whether cities that enact gun control laws saw an increase or a decrease in crime. They also surveyed the participants to determine (a) their political views and (b) some sort of measure of their numeracy. In both the skin-rash and gun-control cases, they had two versions of the question, in which all that was switched was the right answer — that is, they interchanged the labels “Rash got better” and “Rash got worse,” leaving all the numbers unchanged.
The results:
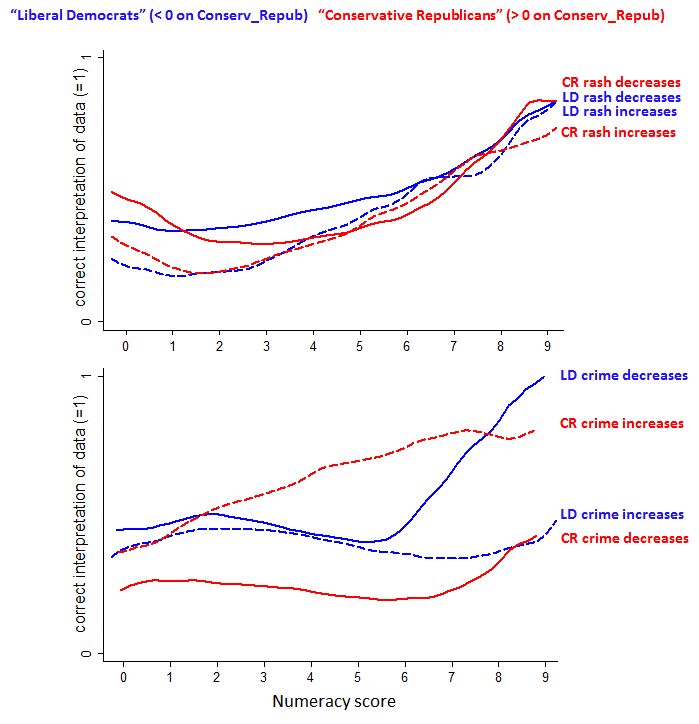
The top graph is for the skin-rash version of the study. The bottom rash is the gun-control version. In time-honored fashion, red is conservative and blue is liberal.
No big surprises in the skin-rash results (except possibly the suggestion that the curves rise a bit at very low numeracy, but I don’t know how significant that is). The action is all in the lower graph, which indicates the following:
- Both liberals and conservatives are more likely to get the answer right when it accords with their political preconceptions.
- For liberals, there’s a large difference only among the highly numerate — the innumerate do equally badly whichever political valence they see.
Fact 1 is interesting but not astonishing. Fact 2 is the really fascinating one.
The proposed explanation:
Our first instinct, in all versions of the study, is to leap instinctively to the wrong conclusion. If you just compare which number is bigger in the first column, for instance, you’ll be quickly led astray. But more numerate people, when they sense an apparently wrong answer that offends their political sensibilities, are both motivated and equipped to dig deeper, think harder, and even start performing some calculations—which in this case would have led to a more accurate response.
“If the wrong answer is contrary to their ideological positions, we hypothesize that that is going to create the incentive to scrutinize that information and figure out another way to understand it,” says Kahan. In other words, more numerate people perform better when identifying study results that support their views—but may have a big blind spot when it comes to identifying results that undermine those views.
What’s happening when highly numerate liberals and conservatives actually get it wrong? Either they’re intuiting an incorrect answer that is politically convenient and feels right to them, leading them to inquire no further—or else they’re stopping to calculate the correct answer, but then refusing to accept it and coming up with some elaborate reason why 1 + 1 doesn’t equal 2 in this particular instance. (Kahan suspects it’s mostly the former, rather than the latter.)
The Mother Jones article suggests that “both liberals and conservatives” show effect number 2 — highly numerate people being more biased than less numerate people — but from the graph the effect seems much smaller for the conservatives. It seems to me that the liberals are the ones whose behavior needs explaining.
With that caveat, this explanation may well be right, but I wonder if there might be other effects. Maybe highly numerate liberals differ from less numerate liberals in some other way, such as more strongly-held political views. I’m not necessarily espousing that speicfic explanation; I’m just wondering. I’d be interested to hear other ideas.
I found the graphs difficult to interpret. Their numeracy measure isn’t equally distributed (it isn’t a percentile), so there isn’t much data in the tails. The graphs are also LOWESS smoothed, which I find intensely annoying–I want to see actual data points with error estimates, any fit or smooth ought to be a *supplement* to the data.
The core of their conclusion would seem to be in figure 7 of the paper, the density distributions derived from their regression model. Those show the “red” population consistently more polarized than the “blue”, which I think does pretty much agree with the other graphs if the population density is taken into account.
I don’t really have a conclusion, other than the usual conniptions I get looking at statistics outside physics. I am somewhat fascinated by the way people apply their prejudices to entirely hypothetical data…
“In time-honored fashion, red is conservative and blue is liberal.”
Note for readers outside the USA (and to those inside): What Ted says is true of the US, where red is the Republican colour and blue the Democratic colour. Almost everywhere else, red is associated with the left: be it social democrats, socialists or communists. There is no particular colour associated with conservatives. (In Germany it is black; I’m sure it’s blue in some places.)
Red used to mean socialist/communist in the US too; the current red state/blue state associations only became widely used during the 2000 election (so not so time-honored).
The US also has its own idiosyncratic meaning for “liberal”–a US liberal is a social democrat in the rest of the world (we also currently don’t have much of a leftist political movement–our democrats are center-right (what the rest of the world would call liberal), and our republicans are closet tories).
That dovetails with what the former Science and Nature editors-in chief wrote in their book “Betrayers of the Truth” (about scientific fraud): when a racist anthropologist published a paper (over a century ago by now) on how the Western brains were the largest and the Hottentots had the smallest, all critics cried foul on political/ethical grounds but, as the authors mention, failed to see the most glaring statistical errors in the paper that would have easily allowed them to defeat it on purely mathematical grounds.