Month: May 2013

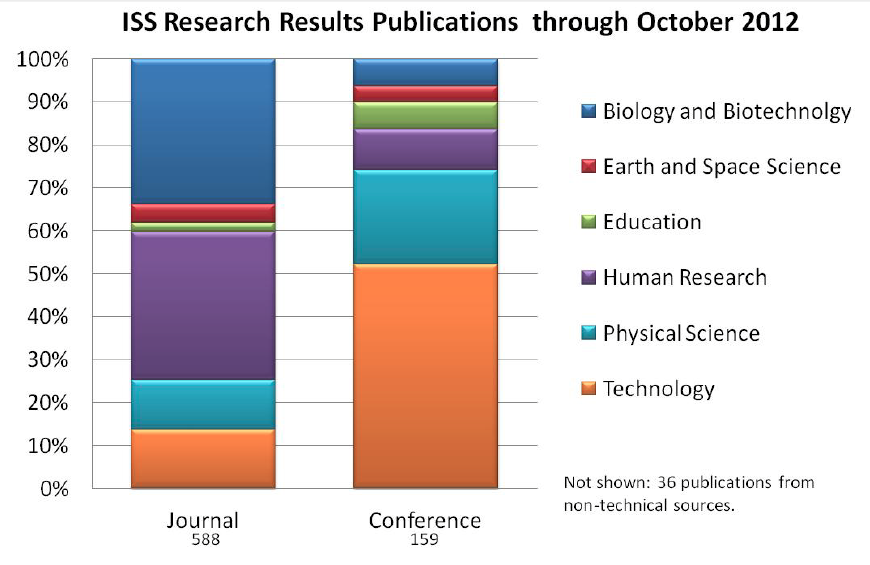
[This starts with some old stuff, well-known to astronomers. A bit of new stuff at the end.]

As everyone knows (except Galileo, who famously got this badly wrong), the Moon causes the tides. The tides, in turn, have an effect on the Moon, causing its orbital radius to gradually increase.  This is, incidentally, a good reason not to miss a chance to see a total solar eclipse like the one that’ll be visible from North America in 2017. Once the Moon gets a bit further away, there won’t be any more total eclipses. I don’t know how many more we have to go, but I know it’s a finite number.

The mechanism goes like this. The Moon’s gravity raises tidal bulges in the oceans. As the Earth rotates, those tidal bulges get ahead of the Moon’s position. The off-center bulges exert a forward force on the Moon, increasing its energy and driving it into a higher orbit:

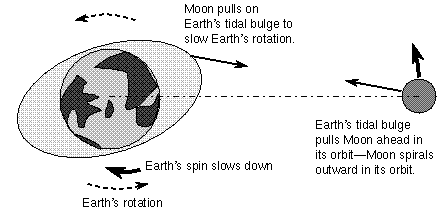
(Picture lifted from here, but where they got it from I don’t know.)

In addition to pushing the Moon into a higher orbit, this also causes the Earth’s rotation to slow down, making the days get gradually longer. To be precise, the Moon’s orbit is getting bigger at a rate of about 4 centimeters per year, and the days are getting longer by about 17 microseconds per year.

Those may not sound like much, but over time they add up. For instance, this is responsible for the fact that we have to introduce leap seconds every so often. When the second was standardized, people tried to make it consistent with the length of the day. But since the early 20th century, the day has gotten longer by a couple of milliseconds. That means that time as measured in seconds drifts with respect to time measured in days. If you let this go on long enough without doing anything, eventually noon would be at night. The master timekeepers have decided they don’t like that idea, so every time things get out of sync by a second (which happens every year or two), they introduce a leap second to bring the clocks back in line.

Here’s another cool consequence of this stuff. A couple of thousand years ago, the days were several seconds shorter than they are now. So an average day over the past 2000 years was about a second shorter than today. If you add up one second per day over the course of 2000 years, you get 2000 x 365 seconds, which is about a week (give or take).

Based on our knowledge of solar system dynamics, we can calculate exactly when a certain event such as eclipses should have taken place. To be precise, we can calculate how many seconds ago the event took place. If you use that to figure out the date on which the event took place, and you don’t take into account the fact that the Earth has been slowing down, you’ll get an answer that’s off by up to a week or so. Sure enough, if you look up the dates of eclipses in ancient Chinese records, the results only make sense if you take account of the Earth’s slowing rotation.

You might not think there’s any way to tell whether days were a couple of seconds longer in ancient times than today, but by letting that tiny difference accumulate over enough years, you can.

That’s all old news. Here’s something new. According to an article in New Scientist, there’s a puzzle about the rate at which the Moon is receding from the Earth:

The moon’s gravity creates a daily cycle of low and high tides. This dissipates energy between the two bodies, slowing Earth’s spin on its axis and causing the moon’s orbit to expand at a rate of about 3.8 centimetres per year. If that rate has always been the same, the moon should be 1.5 billion years old, yet some lunar rocks are 4.5 billion years old.

I can’t make the numbers work out here. 3.8 cm/year times 1.5 billion years is 57 000 km. The Moon is about 380 000 km away. How do we know the Moon didn’t start out more than 57 000 km closer than it is now?

You wouldn’t expect the rate to be constant anyway. My naive guess would have been that, back when the Moon was closer, it dissipated more energy than it does now, so the rate of change should have been greater. If there is an age problem of the sort New Scientist describes, then such an effect would exacerbate it.

According to the article, the solution to this puzzle may be that tides were weaker in the past. A new publication by Green and Huber claims, based on models of ocean dynamics, that tides dissipated considerably less energy 50 million years ago than they do today. That’d mean less Earth slowdown, and less Moon recession. According to New Scientist, 

The key is the North Atlantic Ocean, which is now wide enough for water to slosh across once per 12-hour cycle, says Huber. Like a child sliding in a bathtub, that creates larger waves and very high tides, shoving the moon faster.

If I understand correctly, the idea is that we’re now in a time when a natural frequency of oscillation of the north Atlantic is about 12 hours. This is the same as the rate at which the Moon drives tides (there are two high tides a day). When you drive an oscillating system near one of its natural (resonant) frequencies, you get a big effect, as the makers of the Tacoma Narrows Bridge could tell you.

I guess that’s possible. The resonant frequencies certainly depend on the size of the “container,” and 50 million years ago is long enough that the sizes of oceans were significantly different. Maybe we’ve been moving into a time when the driving of tides by the Moon is near a resonance of the ocean.

 

A couple of people have asked me about the recent gushing piece in the Guardian about the physicist Eric Weinstein, who appears to be claiming to have found a theory of everything.

Here’s the short answer: Read what Jennifer Ouellette has to say. I think she’s got it exactly right.

For those who don’t know, the story goes something like this. Eric Weinstein has a Ph.D. in mathematical physics from Harvard University and left academia for finance a long time ago. He thinks that he has figured out a new theory that would solve most of the big problems in theoretical physics (unification of the forces, dark matter, dark energy, etc.). Marcus du Sautoy, Oxford Professor of the Public Understanding of Science invited him to give a lecture on it. du Sautoy published an op-ed in the Guardian about how revolutionary Weinstein’s ideas were going to be, and Guardian science reporter Alok Jha fulsomely blogged about it.

The  thing that makes this story unusual is that Weinstein has not produced any sort of paper explaining his ideas, so that others can evaluate them.

Incidentally, some people have said that du Sautoy failed to invite any physicists to Weinstein’s talk. (du Sautoy is a mathematician, not a physicist.) That turns out not to be true: du Sautoy did send an email to the Oxford physics department, which ended up not being widely seen for some reason.

Ouellette:

No, my beef is with the Guardian for running the article in the first place. Seriously: why was it even written? Strip away all the purple prose and you’ve got a guy who’s been out of the field for 20 years, but still doing some dabbling on the side, who has an intriguing new idea that a couple of math professors think is promising, so he got invited to give a colloquium at Oxford by his old grad school buddy. Oh, and there’s no technical paper yet — not even a rough draft on the arxiv — so his ideas can’t even be appropriately evaluated by actual working physicists. How, exactly, does that qualify as newsworthy? Was your bullshit detector not working that day?

It was stupid for the Guardian to hype this story in the absence of any evidence that Weinstein actually has anything. If he does, he should show the world, in enough detail that others can check his theory out in detail. At that point, if he’s really got something, hype away!

People often get annoyed when newspapers report on results that haven’t yet gone through formal peer review by a journal. That’s not the point here at all. If Weinstein had a paper on the arxiv explaining what he’s talking about, that’d be fine.

Like Ouellette, I’m mostly irritated by the way the Guardian pieces play into myths about the way science is done:

Furthermore, the entire tail end of the article undercuts everything Kaplan and al-Khalili say by quoting du Sautoy (and, I’m sad to say, Frenkel) at length, disparaging the “Ivory Tower” of academia and touting this supposedly new, democratic way of doing physics whereby anyone with an Internet connection and a bit of gumption can play with the big boys.

It’s disingenuous — and pretty savvy, because it cuts off potential criticism at the knees. Now any physicist (or science writer) who objects to the piece can immediately be labeled a closed-minded big ol’ meanie who just can’t accept that anyone outside the Physics Club could make a worthwhile contribution.

I’m sure it’s true that established physicists tend to pay more attention to people they know, with jobs at elite universities, than to contributions from relatively unknown strangers. That’s human nature. But this is a lousy case study to illustrate this point, at least right now. When Weinstein shows experts his ideas in enough detail to evaluate them, then we can talk.

One of the biggest myths in the popular conception of science is that of the lone genius coming up with brilliant insights with no contact with the established hierarchy. It’s worth remembering that, to an excellent approximation, this never happens. Maybe Weinstein is the exception, but I doubt it.

 

Stephanie Coontz has a piece in the Sunday Review section of today’s New York Times under the headline “When Numbers Mislead” about times when the average of some quantity can prove to be misleading. I’m always glad to see articles about quantitative reasoning show up in the mainstream press, and I think she gets most of the important things right. Way to go, Times!

Coontz starts with the observation that a small number of outliers can make the average (specifically the mean) value different from the typical value: if Warren Buffett moves to a small town, the average wealth goes way up, but the typical person’s situation hasn’t changed. This is familiar to people who regularly think about this sort of thing, but lots of people have never thought about it, and it’s worth repeating.

She then gives an example of a way that this can lead to incorrect policy decisions:

Outliers can also pull an average down, leading social scientists to overstate the risks of particular events.

Most children of divorced parents turn out to be as well adjusted as children of married parents, but the much smaller number who lead very troubled lives can lower the average outcome for the whole group, producing exaggerated estimates of the impact of divorce.

I actually think she’s got something wrong here. I don’t think that using the average unhappiness leads to “exaggerated” estimates. The total unhappiness caused by divorces is the number of divorces times the average unhappiness per divorce. That’s true whether the unhappiness is evenly spread out or is concentrated in a small number of people.

Knowing whether the distribution is smooth or lumpy may well be important — the optimal policy may be different in the two cases — but not because one  is “exaggerated”.

Coontz cites a variety of other examples of times when it’s important to be careful when thinking about averages. For instance, there’s a lot of variation in how people respond to a major loss, so we should be too quick to pathologize people whose response is different from the “usual.”

When we assume that “normal” people need “time to heal,” or discourage individuals from making any decisions until a year or more after a loss, as some grief counselors do, we may be giving inappropriate advice. Such advice can cause people who feel ready to move on to wonder if they are hardhearted.

Another: Married people are happier than unmarried people, but that doesn’t mean that marriage causes happiness. It turns out that the married people tended to be happier before they got married.

The last one is a very important point, but it seems oddly out of place in this article. This is not an “averages-are-misleading” example at all. It’s a classic “correlation-is-not-causation”. These are both important points, but I got kind of confused by the way Coontz blended them together.

By the way, I’m unable to mention correlation and causation without referring to this:

 

Actually, that’s my main quibble with the article: Coontz talks about a bunch of different things (the mean of a skewed distribution is different from the typical value, sometimes variances are large so the mean isn’t typical, correlation is not causation), so the article feels a bit like a grab-bag of pitfalls in statistical reasoning rather than a coherent whole.

But that’s OK: there are lots of worse things you could put in the pages of the Times than a grab-bag of pitfalls in statistical reasoning.

I like to bore anyone who’ll listen with the fact that human space flight, and the International Space Station in particular, are lousy ways to do scientific research, so in fairness I thought I’d point out that NASA has put out a document providing information on the science performed on the ISS.

Much of the information is hard to interpret. For instance, there are graphs quantifying the number of “investigations” performed as a function of time, but it’s hard to know what to make of this, because I don’t know what counts as an investigation.

Here are the research highlights listed:

• Virulence of Salmonella microbes increases in space; researchers have used this discovery to create an approach to develop new candidate vaccines.
• Nutrition studies conducted on the space station show that diets rich in Omega-3 fatty acids are correlated with reduced bone loss.
• Candidate treatments for a form of muscular dystrophy and for testicular cancer have been developed based on space station research results.
• Space station research has involved over 1.2 million students in the U.S., and 40 million more have participated in educational demonstrations performed by astronauts onboard ISS.
• Capillary flow experiments on the space station have produced universal equations for modeling the behaviors of fluids in space.
• The space station serves as a platform to monitor climate change, disaster areas and urban growth on Earth.
• Recent plant studies conducted on the ISS indicate that some of the root growth strategies that had always been thought to require gravity also occur on orbit. This finding provides fundamental insight into the processes of plant growth and development on earth, as well as contributing to our understanding of how best to grow food in space and other novel environments.

I could make snide remarks about some of these, but I won’t. You can decide for yourself how impressed to be. Bear in mind that the cost of the ISS is estimated at $100 billion.

Here is perhaps the most useful quantitative data: scientific publications resulting from ISS research:

If you assumed that the primary purpose of the ISS was to do science, then each journal publication coat about $170 million ($100 billion divided by 588). Even if you assumed that the ISS is 1% about science, it’s $1.7 million per publication, which is an insanely large amount compared to “normal” scientific spending.

The moral of the story: the ISS, and human space flight in general, are not about science. Any science done on them is a side show. I think it’s worth repeating this regularly, because in many peoples minds Space = Science. In particular, I worry that, when people think about the federal budget, more money spent on things like the ISS will mean less money for science.

Daniel Sarawitz, in Nature:

Actually, the bill doesn’t say or imply anything at all about replacing peer review. It doesn’t give Congress new powers over the NSF, nor does it impose on the NSF any new responsibilities. Yes, it requires that the NSF director “certifies” that projects funded by the agency are “in the interests of the United States to advance the national health, prosperity, or welfare”, that the research “is of the finest quality, is ground breaking” and so on. But these vague requirements merely rearticulate the same promises that scientists and government agencies use all the time to justify their existence.

…

In other words, it’s not a very good bill, but neither is it much of a threat.

Sarawitz’s larger point in this article is quite unclear to me. If you want to know what he’s getting at, you’ll have to read it yourself, because I don’t understand it even well enough to summarize it. But at least he’s not spreading the “killing-peer-review” panic.

 

but it’d be even better if he didn’t suck at it.

His latest NY Times column uses trends in the use of various words over time, measured from Google’s NGram data set, as evidence that certain social changes have occurred. Here’s his first main point:

The first element in this story is rising individualism. A study by Jean M. Twenge, W. Keith Campbell and Brittany Gentile found that between 1960 and 2008 individualistic words and phrases increasingly overshadowed communal words and phrases.

That is to say, over those 48 years, words and phrases like “personalized,” “self,” “standout,” “unique,” “I come first” and “I can do it myself” were used more frequently. Communal words and phrases like “community,” “collective,” “tribe,” “share,” “united,” “band together” and “common good” receded.

Similarly, Brooks claims, trends in the use of various words indicate the “demoralization” and “governmentalization” of society: apparently we don’t talk about morals and values anymore, and we  talk more about government.

Coincidentally, these are three of Brooks’s favorite social ills to wring his hands over.

And of course that’s the problem. There are tons of things you could choose to measure, and it’s very easy to convince yourself that you’re seeing evidence for those things you already thought were true. I don’t see any way to turn this sort of playing around into a controlled study, so I don’t see any reason to take this seriously.

Brooks, to his credit, acknowledges this problem. Here’s the last paragraph of his piece:

Evidence from crude data sets like these are prone to confirmation bias. People see patterns they already believe in. Maybe I’ve done that here. But these gradual shifts in language reflect tectonic shifts in culture. We write less about community bonds and obligations because they’re less central to our lives.

The first half of this paragraph, it seems to me, could be summarized as “Never mind all the stuff above.”  Then the second half, citing precisely no evidence, says “But it’s all true anyway.”

Here’s a little illustration of the confirmation-bias problem. For each of Brooks’s three points, I can easily show you similar data that suggest the opposite. In some cases, these are Brooks’s own word choices, for which I can’t reproduce the trends he claims exist. For others, they’re different words with similar valences that show trends opposite to those he claims.

Point 1: we’re more individualized and less community-oriented.

Here are two of the words Brooks claims illustrate this:

See how these have plummeted?

Also, you’d think that along with this trend toward indiviualism we’d be less family-oriented:

Point 2: We don’t talk about morality.

But apparently we do talk about ethics.

Point 3: Government is taking over.

I’m not actually claiming that any of Brooks’s claimed trends is false, just that this is a more than usually silly way of thinking about them. Words come in and out of fashion. Maybe the fact that we talk about morals less and ethics more is telling us something about ourselves as a society, but maybe it’s just linguistic drift.

Nature ran a column by Colin Macilwain under the headline “Driving students into science is a fool’s errand.” Here’s the subhead:

If programmes to bolster STEM education are effective, they distort the labour market; if they aren’t, they’re a waste of money.

(In case you don’t know, STEM = “Science, Technology, Engineering, Mathematics”.)

The key part of the argument:

Government promotion of science careers ultimately damages science and engineering, by inflating supply and depressing demand for scientists and engineers in the employment market.

Start by asking why no such government-backed programmes exist to pull children into being lawyers or accountants. The obvious answer is that there is no need: young people can see the prospects in these fields for themselves. As a result, places to study these subjects tend to be fiercely competitive. But in many science and engineering disciplines, college places are ten-a-penny after decades of sustained government efforts to render them more attractive.

The dynamic at work here isn’t complicated. By cajoling more children to enter science and engineering — as the United Kingdom also does by rigging university-funding rules to provide more support for STEM than other subjects — the state increases STEM student numbers, floods the market with STEM graduates, reduces competition for their services and cuts their wages. And that suits the keenest proponents of STEM education programmes — industrial employers and their legion of lobbyists — absolutely fine.

In short, if we let the free market handle everything, won’t it lead to the optimal number of STEM graduates?

Although my worst grade in college was in Econ 101, I understand the general argument that letting markets freely set prices leads to optimal allocation of resources. I also know that there are a bunch of exceptions to this rule.

In discussions of education, the usual exception people talk about is positive externalities. The general principle is uncontroversial: when an action has benefits that accrue to someone other than the actor, the usual supply-and-demand argument doesn’t properly account for those benefits, and the socially optimal amount of that action is larger than what the market will naturally lead to. You get some benefit from vaccinating your kid against whooping cough, but so do your neighbors. Even if the cost of the vaccine isn’t worth it to your family, it may be worth it to society. The solution is to subsidize or legally require vaccinations.

(Of course there are also negative externalities, the classic examples being pollution and traffic congestion. In those cases, the actor doesn’t bear the full cost of the action, so to attain the socially optimal outcome the government must tax or regulate.)

We don’t leave education up to the free market — we legally mandate it and publicly fund it — at least in part because of the belief that education has positive externalities. People who can read are better citizens, which benefits us all.

Sometimes (e.g., in Wikipedia, but I’ve also seen it a bunch of other places), people say that a positive externality of education is that it makes people more productive workers:

Increased education of individuals can lead to broader society benefits in the form of greater economic productivity, lower unemployment rate, greater household mobility and higher rates of political participation.

Italics added. Presumably if you want to counter Macilwain’s argument with an externality-based argument, you’d emphasize that sort of thing.

Maybe I’m betraying my ignorance of economics, but I don’t understand how those two (high productivity and low unemployment) are externalities. It seems to me that those should be priced into the free-market calculation. That is, if STEM graduates have high productivity, they’ll command high salaries. This benefit accrues to the STEM graduate, so it’s not an externality, and the classical free-market economics argument should hold. I’m pretty sure that’s what Macilwain woulds say, and I don’t think he’s wrong about that.

I actually don’t think that positive externalities are the best argument in favor of programs to encourage STEM education. The real reasons, it seems to me, have to do with the sorts of things behavioral economists like to talk about.

Old-fashioned economics, including the argument that the free market optimally allocates resources, is based on a model in which individuals act rationally to optimize their own self-interest. If an engineering degree will lead to the greatest possible happiness later in life, then you’ll choose to get an engineering degree. If not, not.

Behavioral economics is based on the obvious observation that people don’t really act in their own rational self-interest all the time. I think that the best argument in favor of programs to steer students toward STEM education is based on this observation. Some students might not realize that a STEM career is a good option (or even a possible option) for them, especially early on in their education. If that’s true, then the free market will underproduce STEM graduates (compared to the socially optimal level), and we should find ways to bump up the numbers.

 

I haven’t been able to work up much umbrage over the proposed move by  Republican Congressman Lamar Smith to change the way the National Science Foundation grants are awarded. I think that the proposed changes are a bad idea, but would have much less practical effect than some people claim.

Via Phil Plait, I see that the Canadian government seems to be actually doing what people hyperbolically claim the Smith bill would do:

The government of Canada believes there is a place for curiosity-driven, fundamental scientific research, but the National Research Council is not that place.

“Scientific discovery is not valuable unless it has commercial value,” John McDougall, president of the NRC, said in announcing the shift in the NRC’s research focus away from discovery science solely to research the government deems “commercially viable”.

I don’t know enough about Canadian science, or Canadian government workings in general, to be sure, but this sounds exactly like what Lamar Smith wants to do in the US. The difference is that it appears to be actually happening in Canada, whereas even if Smith’s bill were to pass, I don’t think it would have the effect he’s aiming for.

Perhaps the most shocking thing about this is that it’s being done with the approval of the head of the National Research Council, who actually said

“Scientific discovery is not valuable unless it has commercial value.”

It’s easy to imagine this sentence coming out of the mouth of a member of the US Congress,  but not from the head of, say, the National Science Foundation.

Phil Plait on why this is wrongheaded:

This is monumentally backwards thinking. That is not the reason we do science. Economic benefits are results of doing research, but should not be the reason we do it. Basic scientific research is a vast endeavor, and some of it will pay off economically, and some won’t. In almost every case, you cannot know in advance which will do which.

In the 19th century, for example, James Clerk Maxwell was just interested in understanding electricity and magnetism. He didn’t do it for monetary benefit, to support a business, or to maximize a profit. Yet his research led to the foundation of our entire economy today. Computers, the Internet, communication, satellites, everything you plug in or that uses a battery, stem from the work he did simply because of his own curiosity. I strongly suspect that if he were to apply to the NRC for funding under this new regime, he’d be turned down flat. The kind of work Maxwell did then is very difficult to do without support these days, and we need governments to provide that help.

 

 

I’ve always liked Feynman’s quote about the relationship between science and beauty. (I mentioned it once before.) Someone’s made an animation to go along with the original audio of Feynman saying it. Check it out:

 

 

 

The New Yorker has a piece up about how Lamar Smith’s new bill will get rid of peer review at the National Science Foundation. As far as I can tell, the bill would do no such thing.

Currently, proposals are evaluated through a traditional peer-review process, in which scientists and experts with knowledge of the relevant fields evaluate the projects’ “intellectual merits” and “broader impacts.” Peer review is a central tenet of modern academic science, and, according to critics, the new bill threatens to supersede it with politics.

This paragraph would be fine, if it were followed by a clear statement that the last sentence, while it may be true “according to critics” is not, you know, actually true. There’s nothing in the text of the bill that can reasonably be described in this way.

If I were full of nostalgia for the glory days of the New Yorker, I’d say something at this point about William Shawn spinning in his grave, but I’m not, so I won’t.

(Just to shore up my anti-Republican bona fides, let me repeat some things from my earlier post. Despite the fact that this bill is being mischaracterized by its critics, it’s still a bad idea, and Lamar Smith and many of his fellow Congressional Republicans are indeed Enemies of Science.)