I’m teaching our course in Electricity and Magnetism this semester, and even though I’ve done this plenty of times before, I still learn new things each time. Here are a couple from this semester.
1. Charged conducting disk.
Suppose I take a thin disk of radius R, made out of a conducting material, and put a given amount of charge Q on it. How does the charge distribute itself? (In case it’s not clear, the disk lives in three-dimensional space but has negligible thickness. In other words, it’s a cylinder of radius R and height h, in the limit h << R.)
This turns out to have a surprisingly simple answer. Take a sphere of radius R, and distribute the charge uniformly over the surface. Now smash the sphere down to a disk by moving each element of surface area straight down parallel to the z axis. The resulting charge density is the answer.
My friend and colleague Ovidiu Lipan showed me a proof of this, and then I verified it numerically using Mathematica, so I’m confident it’s right. But I still have the feeling there’s more to the story than this. This result is simple enough that it seems like there should be a satisfying, intuitive reason why it’s true. Although Ovidiu’s proof is quite clever and elegant, it doesn’t give me the feeling that I understand why the result came out in this neat way. I’d love to hear any ideas.
Update: These notes by Kirk McDonald have the answer I was looking for. I’ll try to write a more detailed explanation at some point.
2. Electric field lines near a conducting sphere.
Take a conducting sphere and place it in a uniform external electric field. Find the resulting potential and electric field everywhere outside the sphere.
This is a classic problem in electrostatics. I’ve assigned it plenty of times before, but I learned a little something new about it, once again from the exceedingly clever Ovidiu Lipan (who apparently got it from an old book by Sommerfeld).
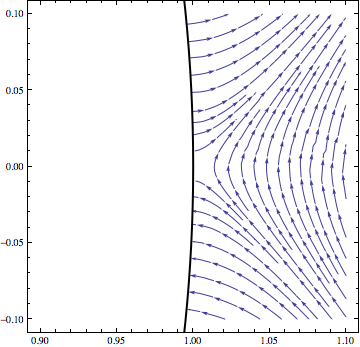
You can calculate the answer using standard techniques (separation of variables in spherical coordinates). The external field induces negative charge on the bottom of the sphere and positive charge on the top, distorting the field lines until they look like this:
This picture looks just as you’d expect. In particular, one of the first things you learn about electrostatics is that field lines must strike the surface of a conductor perpendicular to the surface.
Let’s zoom in on the region near the sphere’s equator:
The field lines either strike the southern hemisphere, emanate from the northern hemisphere, or miss the sphere entirely. All is as it should be.
Or is it? Let me put in a couple of additional field lines:
The curves in red are legitimate electric field lines (i.e., the electric field at each point is exactly tangent to the curve), but they don’t hit the surface at a right angle as they’re supposed to. You can actually write down an exact equation for these lines and verify that they come it at 45-degree angles right up to the edge of the sphere.
We constantly repeat to our students that electric field lines have to hit conductors at right angles. So is this a lie?
Ultimately, it’s a matter of semantics. You can say if you want that those red field lines don’t actually make it to the surface: right at the sphere’s equator, the electric field drops to zero, so you could legitimately say that the field line extends all the way along an open interval leading up to the sphere’s edge, but doesn’t include that end point. This means you have to allow an exception to another familiar rule: electric field lines always start at positive charges and end at negative charges (unless they go to infinity). Here we have field lines that just peter out at a place where the charge density is zero.
Alternatively, you can say that there’s an exception to the rule that says electric field lines have to hit conductors at right angles: they have to do this only if the field is nonzero at the point of contact. After all, the “must-hit-perpendicular” is really a rephrasing of the rule that says that the tangential component of the electric field must be zero at a conductor. The latter version is still true, but it implies the former version only if the perpendicular component is nonzero.