I’m giving a talk here in Paris tomorrow on the question of how to interpret the cosmological redshift. The talk is based on the paper David Hogg and I wrote last year. I said a bit about the argument of the paper in a previous post. I’ll quickly recap the big idea, but then I want to comment on some followups to our paper: a blog post by Sean Carroll (from way back when we first posted our paper) and a recent paper by MichaÅ‚ Chodorowski.
First the background. The most important fact in cosmology is that the light from distant galaxies is redshifted. This fact is the observational basis for the idea of the expanding Universe. Most of the time, when you see a redshift, it’s a Doppler shift — that is, it’s caused by the fact that the observed object is moving away from you. In the cosmological context, though, people often say that the observed redshift has a different explanation: they say that the galaxies aren’t “really” moving, but rather that space itself is expanding, which causes the light to be stretched out in wavelength. Hogg and I argue for the rehabilitation of the idea that the galaxies are moving and the observed redshift can be regarded as a Doppler shift.
The main thing to realize about all this is that we’re talking purely about a question of interpretation: everybody (at least, everybody sane) agrees on the physics — the argument is only about what words to wrap around the physics. Sean Carroll expressed this well in his blog post:
These are not arguments about the theory €” everyone agrees on what GR predicts for observables in cosmology. These are only arguments about an analogy, i.e. the translation into English words.
…
The point is, arguments about analogies (and, by extension, the proper words in which to translate some well-accepted scientific phenomenon) are not "right" or "wrong." The analogies are simply "useful" or "useless," "helpful" or "misleading." And which of these categories they fall into may depend on the context.
This is 100% right. We argue in our paper that the expanding-space picture in cosmology (particularly the metaphor of a stretching rubber sheet or balloon) is misleading, in that it leads people to some incorrect intuitions about the nature of space, and we try to suggest different a way of looking at things. But our way has its flaws too: all of these verbal descriptions are at best incomplete at capturing the whole picture. We try to argue forcefully in favor of our way of looking at things, but the truth is that I’d be happies if people are exposed to several different ways, not just ours.
Here’s something else Sean says:
On the other hand, there is another pernicious mistake that people tend to make: the tendency, quite understandable in Newtonian mechanics, to talk about the relative speed between two far-away objects. Subtracting vectors at distinct points, if you like. In general relativity, you just can't do that. And realizing that you just can't do that helps avoid confusions along the lines of "Don't sufficiently distant galaxies travel faster than light?" And reifying a distinction between the Doppler shift and the cosmological redshift is a good first step toward appreciating that you can't compare the velocities of two objects that are far away from each other.
The beginning of this is exactly right: A central idea of general relativity is that you can’t compare vectors at distant points, which means that there’s no well-defined way to talk about the velocity of A relative to B, when A and B are far apart. But I think he goes completely off the rails in the last sentence.
Sean seems to think that the expanding-rubber-sheet metaphor helps to convey the idea that you can’t talk about velocities of distant objects, but I think it does precisely the opposite. The rubber-sheet picture virtually demands that you think of things that are just sitting still on the rubber sheet as being “really” at rest. In its most extreme form (found in a lot of textbooks and pop-science books), the rubber-sheet metaphor says that distant galaxies are not moving with respect to us — that is, not that their velocities with respect to us are undefined, but that they’re zero!
In effect, the rubber sheet acts in people’s minds like a sort of aether, i.e., a preferred frame to use in defining all motions. This is precisely the opposite of how you want to understand space in relativity.
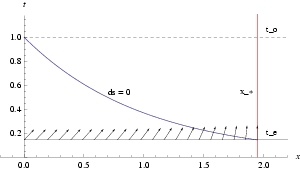
Anyway, that post of Sean’s is ancient history (more than a year old). Here’s something much more recent: the paper by Chodorowski called “The kinematic component of the cosmological redshift.” Chodorowski adopts a similar philosophy to us in some ways: he, like us, observes that if you want to talk about the velocity of a distant galaxy, you need to adopt a prescription for “carrying” its velocity vector over to us. But while we argue that the most natural prescription is to carry the vector along the light path, he says that it’s more natural to carry the vector from one location to the other at a fixed moment in time. Figure 1 of his paper illustrates this:
I tend to disagree with his assessment of which path is more natural. The reason is that the comparison we want to make is between the galaxy’s velocity at the time of emission and our velocity now. That is, the two vectors we want to compare live at the lower right and upper left of his diagram. If you follow Chodorowski’s path from right to left across the bottom, you then have to make a right turn and head up the t axis. (He also considers the alternative where you go straight up first and then across.) My preferred path is along the solid curve in the figure.
But the truth is that these “naturalness” questions are always matters of taste. Chodorowski’s point of view is a very reasonable and sensible one, and this is a very nice paper.
Chodorowski’s two options correspond in effect to figuring out (a) the relative velocity of the galaxy and us back then (at the time of emission), and (b) the relative velocity of the galaxy and us now. Hogg and I calculate something that can best be described as (c) the velocity of the galaxy then relative to us now. In my dream world, people who want to understand the nature of the redshift would examine what happens when you do all three possibilities, and why they’re different.
First, I agree that there is agreement over the actual physics and that it is a matter of interpretation. However, the statement
Hogg and I calculate something that can best be described as (c) the
velocity of the galaxy then relative to us now.
illustrates what I think is a shortcoming of your approach. Velocity is distance per time. In cosmology, we have to ask “which distance” and “which time”. There are various distances used in cosmology (proper distance, luminosity distance etc) but as far as I know there is no concept of time which is used for anything else such that one of these distances per this time results in a velocity which is related to the redshift via the Doppler formula (relativistic or not).
In other words, is this velocity of the galaxy then relative to us now used in any context other than that in your paper?
Another way of putting it: Is your concept good enough that it outweighs the pitfall of thinking that the Doppler formula can be used to calculate a useful velocity in cosmology, or, worse, that at high redshift the relativistic Doppler formula must be used. (Since it doesn’t contain the cosmological parameters, it must deliver the same results for all cosmological models, which is almost a reductio ad absurdum argument.)
Note that v = HD is exact for all redshifts and all cosmological models. It doesn’t apply to “directly observable” quantities, but does apply if D is the conventional proper distance in relativity and and v is its derivative with respect to cosmic time as measured now (H is of course the Hubble constant). Thus, it is something people can imagine, if not something one can observe directly at the telescope (whatever that means); this equation doesn’t contain the redshift.
Another way of looking at things: is the “shut up and calculate” approach better or worse than having a “physical idea” of what is going on (I’m thinking of things like Milne’s world map and world picture)?
Again, it’s not the calculations, it’s the mental picture. In this context, do you think there is anything wrong, or even misleading, about Harrison’s classic paper http://adsabs.harvard.edu/abs/1993ApJ…403…28H
I think you provide a very cogent argument in favor of the position that there is NO SUCH THING as the velocity of a distant galaxy relative to us, of the sort that would be useful in describing the redshift. This is in fact the only completely true and defensible position. It leads to the “shut up and calculate” position on the interpretation of the redshift: don’t interpret it at all.
As far as I’m concerned, the whole argument is about what to do if you insist on interpreting the redshift — that is, if you insist on asking what the “right” number to use for the relative velocity is. Between you and me, I don’t think that the picture we describe in our paper is the only correct one, and I’m well aware that it has some flaws (as all such pictures do). What I do think is that the stretching-rubber-sheet one is far too dominant and leads to extremely incorrect intuitions about lots of stuff. Since it’s the one you see wherever you look, I think it’s important to look at others as a corrective.
I think this is really my answer to your question about whether it’s better to have a physical picture or not. My answer is that it’s better to have multiple physical pictures, each imperfect.
You say that “V=HD is exact.” That’s true if you define velocity to mean the change in distance-as-measured-at-fixed-cosmic-time with respect to cosmic time. But that’s manifestly not the relevant concept of velocity to use when interpreting the redshift, though, mostly because we want to compare source and observer at different cosmic times. So V=HD is irrelevant.
You ask my opinion about Harrison’s paper. I read it a long time ago, and took a quick look through it just now but didn’t reread it carefully. The equations certainly all seem true, and I can’t find anything objectionable in it. I’m not completely sure what I’m supposed to get out of this paper, though. How is it supposed to change my view of anything?
Harrison’s paper isn’t supposed to change your view of anything. It’s perhaps not directly relevant to the question of how to interpret the relationship between velocity and redshift, but points out that even such basic things as “Hubble’s Law” are understood to mean different things by different people, and gives an example of what can and cannot be extrapolated from negligible redshifts to cosmologically significant redshifts. He derives the same results with the expanding-space paradigm and the “shut up and calculate” approach. So it’s not completely unrelated. Of course, his point that there is a well defined redshift-distance law (observed by Hubble) and velocity-distance law (a trivial consequence of isotropic and homogeneous expansion) but, since different distances are involved, one can’t simply combine them to get a redshift-velocity law, is relevant to your blog post since this is the source of much of the confusion involving whether or not the idea of a Doppler shift and/or the Doppler formula is appropriate in a cosmological context.
I’m curious as to why all of those in this discussion choose to accept the notion that the redshift relates to cosmological motion, doppler-caused or expanding-space caused. While I believe the redshift does correlate to distance from the remote galaxy to ours, might there not be anther simpler cause of the perceived redshift. Hubble himself was never convinced the redshift he ‘discovered’ related to motion and took this belief to his deathbed. I have my own theory, but not being a trained cosmologist, I am reluctant to share it with professionals until I can tie it down with specialists.
Joel Levinson
Founder: SpaceGroup
Many people have proposed alternate explanations for the cosmological redshift, but all have been found wanting, mainly because they predict additional effects which are not observed. Also, since it is rather straightforward to show that a cosmological redshift exists in an expanding universe, then one has to explain why this shouldn’t be the case. If the explanation is that the universe is not really expanding, then one has to take all the problems into account which this would imply.
Hubble did indeed doubt that the expansion was real towards the end of his life, but this was due to some technical errors involving the K-correction. Had these been solved during Hubble’s lifetime, his doubts would probably have disappeared. This is described in Alan Sandage’s section in THE DEEP UNIVERSE: http://adsabs.harvard.edu/abs/1995deun.book…..S
I don’t see how you can share it with professionals before you tie it down with specialists. In other words, what is the difference between a professional and a specialist?
Just a quick note to agree with Phillip in his response to Joel Levinson. The standard (expanding-universe, general-relativistic) understanding of the redshift agrees with tons of observational data: it’s a very well-tested scientific model. That doesn’t mean that it can’t be wrong, but it does mean that the bar is set VERY high for any alternative theory. Lots of people have thought hard, for close to a century, about alternatives, but none of them have proved viable. If you think you have a viable alternative, frankly, the odds are against you.
By the same token, if you come out openly with it, either someone else has already thought of it or they haven’t. If so, then it has been debunked, and you wouldn’t have had priority anyway. If not, it must be rather bizarre (otherwise someone else would have thought of it), so as long as you publicly announce it, there is no danger that someone else could pass it off as his own work (since it wouldn’t be believable for someone else to present the same bizarre explanation shortly after you make yours public).
There are well known cosmology textbooks that describe electromagnetic waves as having been "stretched" by space due to the expansion of the universe, with a resultant "loss of energy" of photons as the wavelength has been increased.
My interpretation of your paper and the paper of Chodorowski suggest that the redshift of a remote galaxy is due to the observations having been made in a different reference frame to that of the remote galaxy. If this interpretation is correct then there is no loss of energy of the electromagnetic wave and no stretching caused by an unspecified mechanism
Can you advise me on this interpretation please.
Stan–
I think you’ve got it.
The “purist” position goes something like this. It only makes sense to talk about changes in energy if all measurements are made in the same inertial reference frame. When a photon travels over a cosmologically large distance, there is no inertial reference frame that accommodates both the emission and absorption events. Therefore, the question of whether the photon has or has not lost energy is simply meaningless.
When people use the “stretching-of-space” language, they’re implicitly assuming that comoving coordinates (i.e., a coordinate system in which both the emitting galaxy and the observer are at rest) are the most natural ones to use. But comoving coordinates are not an inertial system — that is, they’re not a system in which it makes sense to compare energies at widely different locations. So when people say that the photon has lost energy, they are committing at least a minor sin against general relativity.
Now what about my (and Hogg’s) position? We certainly agree that, if both the observer and emitter measure the photon’s energy (each in his own local inertial frame), the observer’s measurement will come out smaller than the emitter’s. But we think that that difference is more like a Doppler shift than anything else — that is, as you say, that it’s due to relative motion rather than to anything happening to the photon en route.
To expand on this a bit, suppose I throw a baseball to you, and you’re running away from me as you catch it. The baseball’s speed relative to you will be less than its speed relative to me. If each of us computes the ball’s kinetic energy, you’ll get a lower number than me. But it would be perverse to say that this means the ball has lost energy; rather, it’s just that we measured energy in different frames, which can’t reasonably be compared.
Thanks for your guidance on this topic. I have a follow up question.
In an empty universe the cosmological redshift would be entirely a Doppler shift. Our universe is not empty but the WMAP measurements seem to show that the observable universe is flat. Does this not mean that the cosmological redshift must be predominately Doppler?
(My time zone is GMT)
Stan–
In an empty universe, spacetime is flat. In our Universe, space is (very close to) flat. Those are actually quite different statements: our flat-space universe does have significant spacetime curvature. Your observation that in an empty universe the redshift is a Doppler shift is quite correct, but this only applies to a flat-spacetime universe, so it doesn’t apply to our (flat-space but not flat-spacetime) Universe.
The terminology is annoying, but there it is.
Question from a non-physics layperson:
Having just finished Iain Nicolson’s fascinating “Dark Side of the Universe” I found this thread in an attempt to learn more about a statement the author makes regarding the apparent loss of photon energy as space expands (page 142):
“…each time the expansion of the universe stretched the diameter of that region of space by a factor of two, it’s volume would increase by a factor of eight and the number of matter particles and photons in each cubic metre would reduce by a factor of eight. But whereas the density of matter decreases in proportion to the cube of the expansion factor the energy density of radiation decreases with the fourth power of the expansion factor. The reason for this is that, not only does the number of photons in each cubic metre of space decline with the cube of the expansion factor, but radiation is also redshifted by the stretching of space, so that the energy associated with each photon is correspondingly reduced. Each time the size of the universe is doubled, the wavelength of a photon is doubled and its energy halved.”
My curiosity lies in where the energy goes to, which Nicolson does not expand on. Since space seems to be uniformly anthropic, all observers in all galaxies are experiencing the same redshifted light; the explanation that the loss of energy is only apparent doesn’t seem logical to me.
The short, strange answer to the question of where the energy goes is that it doesn’t go anywhere! The total energy of the expanding universe is not conserved. Considering how central the concept of energy conservation is to physics, this fact is quite astonishing — on quite a few occasions, I’ve mentioned it to professional physicists and been flat-out disbelieved at first. But it’s true.
I wish I knew a good not-very-technical explanation of this fact, but I don’t. Way back in the old days of Usenet newsgroups, this was a Frequently Asked Question on the physics newsgroups. The attempt to answer it in the FAQ list can be found at
http://www.desy.de/user/projects/Physics/Relativity/GR/energy_gr.html
But there’s a lot more that could be said on the subject. Some time I should try to write something up on this.
Thank you for the reply. I glanced at the link, but as the technical aspect far outweighs my acumen it will require much more time to fully digest, even on the rudimentary level I’m accustomed to! You’re right, though; this seems quite astonishing to me — much harder to digest than a simpler explanation such as photon energy being absorbed quanta-by-quanta to create vacuum energy, or some other explanation that fits observed phenomena.
Regards,
Mark
Sean Carroll wrote about non-conservation of energy in general relativity here:
http://preposterousuniverse.blogspot.com/2004/05/energy-and-intelligence.html
There’s still more that could be said, and maybe I’ll try to get around to writing something about it some time, but this is a better starting point than the FAQ entry I pointed to before.
You make some good points. I guess this will depend on your standpoint. – You can live to be a hundred if you give up all the things that make you want to live to be a hundred. – Woody Allen Born 1935
I was wondering if you could take a moment to explain section 2 of the original paper you and David posted. I understand the concept that in the Riemann normal coordinates, the galaxy that is stationary in comoving coordinates is moving, and this is something that my gut agrees with; after all, comoving coordinates are supposed to describe the universe as a whole, right?
I’m mostly confused about the jump from equation 2 to equation 3. My gut wants to say that dT = a dt, but this gives results that are unphysical and/or flat-out wrong. Most of the papers in your bibliography inspire various parts of the paper, but I can’t find the inspiration for section 2’s approach. Is there such a paper, and would you mind pointing to it for further edification?
Thanks, that is a great explanation.