What happened 10/10/2017
We began today’s class by going through the challenge problems. While we were talking about problem number 3, an interesting issue came up, which is how do we define the domain of a function. After our discussion, we found out that the domain of a function is not determined by the formula. Instead, the domain is just defined by us. If we say a function f maps from R to R, then the domain of f is R despite the fact that there is certain element in R that f is not defined with.
After we finished talking about the challenge problems, we moved on to our lecture and learned the way of proving functional limit using precise definition. The example we have is to prove . One thing that needs to be paid attention to in this example is that, even though we have
, we should still choose
.
Finally, we talked about theorem 4.2.3, which states that Given and $c\in L(A)$.
if and only if
such that
and
.

Thank you for the synopsis of class, Nicholas. . An important realization is that NOTHING in our proof requires that
. An important realization is that NOTHING in our proof requires that  needs to be SMALL… We want to prove that a viable value for
needs to be SMALL… We want to prove that a viable value for 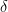 can be chosen FOR ALL possible
can be chosen FOR ALL possible 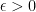 .
.
I hope that you see WHY you should choose
It is natural, as one goes through these proofs, to only fixate on “arbitrarily small” values for , but this does not mean that the proof can ignore the possibility of these values being quite large as well.
, but this does not mean that the proof can ignore the possibility of these values being quite large as well.