Muddiest Point 9/28/2017
I think the muddiest point from Thursday’s class is the distinction between sequences and sets that came from the opening situation. This muddiness most likely comes from our extensive discussions about sequences in the previous weeks, so we are still thinking in terms of sequences instead of now moving on to sets. Further confusion may arise from the connections between sets and sequences in many of the theorems in Chapter 3. We often talk about the sequences contained in a set to make conclusions about the set itself.
The important distinction to make between sets and sequences is that sequences have an ordering while sets do not. I think this distinction can be hard to separate when we are thinking about a set of numbers since there does exist an innate ordering of numbers. When we have the set {1,2,3} it is easy to think that it is ordered because they do happen to be in order from least to greatest. It is important to see that the set {1,2,3} is the same as the set {2,1,3}. On the flip side, {1,2,3} as a sequence is different from {2,1,3} as a sequence.
So to try and keep these straight, think of these as a collection of books instead of numbers. Your entire collection of books is the set. There is no innate ordering; they are just a bunch of books you have. Now imagine you choose all of the science fiction books in your collection and order them by their publication date. Now you have a sequence that is contained in your set.

Excellent post, Rhiannon.
This is, indeed, a common point for confusion, and something that all students should be diligent to keep clear as they work through this material.
Another thing that helps is common notation: We usually note sets with curly braces: {1,2,3} = {2,1,3}, while ORDERED sets (and sequences) usually have parentheses: (1,2,3)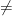 (2,1,3).
(2,1,3).