1st Class – Tuesday, 29th September
In this post, I will discuss the following definitions we covered in the class: Upper Bound, Least Upper Bound (Supremum), and Axiom of Completeness (AoC). I will try to provide a proof template for most of the definitions I state.
1. Upper Bound
If set A is a subset of ℝ, then a number b is called an upper bound for A if it is equal to or greater than all the elements of A. We say that A is bounded above if such a number exists.
Proof template:
Let a in A and b in ℝ, then if b is greater than or equal to a we say that b is an upper bound for A. This holds because a was chosen arbitrarily.
2. Least Upper Bound
A real number s is the least upper bound for a set A in ℝ if it meets the following criteria:
(i) s is an upper bound for A,
(ii) if b is any upper bound for A, then s is less than or equal to b.
Proof Template:
Let a in A, then if s is greater than or equal to all the elements in A it is an upper bound for A. Thus, s meets the first criteria of the above stated definition. Now let’s assume there exist any other upper bound b. If s is less than or equal to b, then we can conclude that s is the least upper bound for A.
3. Axiom of Completeness
Every nonempty set of real numbers that is bounded above has a least upper bound.
Sami
Good exploration of proof templates for these conclusions. Thank you Sami.
I want to point out one technical issue with your templates, which could lead to confusion when constructing proofs with universal quantifiers. For example, consider your proof that b is an upper bound for A. You should avoid the temptation of saying that b is an upper bound immediately after concluding
. Instead, shift your conclusion slightly to say “Since 
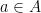was chosen arbitrary, we have shown 
, and so b is an upper bound of A.”
It is subtle, but notice that I carefully identified that b satisfied a universal property on A first, before concluding b was indeed an upper bound. This subtlety may strike you as ridiculous at the moment, but noticing this difference now will help tremendously when we get into more convoluted arguments in the future.