I remember when I started learning mathematics in elementary school, particularly counting the number of balloons on a printed piece of paper and writing that number down at the bottom. Fast-forward 15 years, and I’m in college studying about set theory and still counting – this time the elements in a set, also called the cardinality of that set. But how exactly would you count the elements in an infinite set? An example is the set of natural numbers {1,2,3,4,5,…}. We mathematicians have given the cardinality of such a set the symbol, , pronounced aleph-naught. So what’s so special of this I hear you ask. Well, it’s not only the cardinality of the set of natural numbers, but it is also equal to the cardinality of the set of rational numbers as well as the integers.

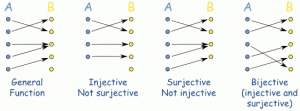
Before we go any further, let’s look at what bijection, surjection, and injection mean (this is for all the non-math people over here, those who already know these terms can jump to the next paragraph). A function (f: A B) is surjective if every element of B is mapped to by at least one element of A. A function (f: A  B) is injective if no two elements of A are mapped to the same element of B. A function (f: A B) is bijective if the function is both injective and surjective. A bijection establishes a one-to-one correspondence between the elements of A and B. So giving an example of infinite sets: cardinality(A) < cardinality(Power Set of A). (See the definition of Power Set below.) This greater signs means that there exists a function from f:A P(A) is injective but none that are surjective, so not all elements of P(A) can be mapped onto. An example is shown below:

If you think blew your mind, wait until I tell you about real numbers and power sets. Georg Cantor actually showed that the cardinality of the real numbers(given the symbol c) is greater than the cardinality of the natural numbers(so there exist mappings from the natural numbers to the real numbers that are injective but none that are surjective), but just how greater are we talking about? Well, the cardinality of the reals is equal to the cardinality of the power set of the natural numbers. WOW!!! (Definition of a Power Set of A: The set of all subsets of A). So now you must be thinking that the set of real numbers may be the biggest set of all. But it doesn’t end there…Cantor actually showed that there are sets greater than the reals, and there is actually no set with the biggest cardinality. How do you do that? Just take the power set of a set and you will keep getting sets with cardinality greater than the previous set. So if someone comes to you and says he has found the set with the greatest cardinality of all time, you know what to do: just take the power set of that set and tell him now you have a set with cardinality greater than his. So are there any other ways besides taking the power set to get a set with greater cardinality? Surely taking the union of two sets of the same cardinality will lead to set with a greater cardinality than the former two, but that it is not the case – the cardinality of the new set will be equal to the cardinality of the former two. So taking the union of the sets of rational numbers with any other countable set gives another countable set, instead of a set of greater cardinality as you might intuitively think. Well that’s more fun things to add to your list of why you like  so much.

Coming back to the cardinality of the natural numbers and real numbers, one question which even confused Cantor was the existence of a set which had a cardinality between the natural numbers and the real numbers. This means a set, let’s call it X, such that the function from the natural numbers to that set X is injective but not surjective, and the function from X to the real numbers is injective but not surjective. This is called the continuum hypothesis which formally states: There is no set whose cardinality is strictly between that of the integers and the real numbers. Cantor spent a lot of time working on this problem. In fact he thought he had proved it false, then the next day found his mistake. Again he thought he had proved it true only again to quickly find his error. The problem remains unsolved even after his death. In 1940, Kurt Godel showed that the Continuum Hypothesis can not be disproved by the axioms we have today. In 1963, Paul Cohen showed that the Continuum Hypothesis can not be proved either.

There you have it folks, everything you need to know about cardinal numbers and how it changed the very foundation of mathematics, and it would not be wrong if you changed your favorite mathematician to Georg Cantor instead. You may think that Cantor was given fame and money throughout his life for his breakthroughs, and died a man content with his life. Instead all of his friends abandoned him, he suffered mental illness, and died in a mental hospital in 1918….mathematics sure can do a lot to a person.