This semester we had 15 Learning targets to cover, including 7 labs and 3 journals: Below is what we were expected to have known by the end of the semester, today lol:)
Calculus Topics
LT1 I can evaluate integrals using substitution and integration by parts and explain which technique is appropriate and why.
LT2 I can apply numerical techniques (left, right, midpoint, trapezoid, and Simpson’s rule) to estimate definite integrals.
LT3 I can compute the area of a region bounded by two curves, including determining whether to integrate with respect to x or y.
LT4 I can compute the volume of a solid using integrals, whether the solid is generated by rotating a function around the x-axis or the y-axis.
LT5 I can use definite integrals to solve problems involving physical or biological systems.
LT6 I can evaluate improper integrals.
LT7 I can check whether a function is a solution to a differential equation and explain why the function is or is not a solution.
LT8 I can use slope fields to obtain qualitative information about the solutions to a differential equation. I can identify stable and unstable equilibria of an autonomous differential equation.
LT9 I can use Euler’s method to approximate the solutions to initial value problems.
LT10 I can solve a separable differential equation.
LT11 I can express real-world situations as differential equations, and interpret differential equations in a biological context.
LT12 Given appropriate information about a function, I can find its Taylor polynomials at a given center a.
LT13 I can determine whether or not an infinite series is geometric and, if so (and it converges), I can find its sum.
LT14 I can use find the Taylor series of one or more familiar functions to find the Taylor series for a related function.
LT15 I can use calculus to model chemical reactions and enzyme kinetics.
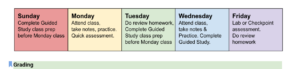
The picture below is derived from Dr Toress’s Math 212 syllabus