I recently mentioned a couple of new things I’d learned in teaching an electricity and magnetism class this semester. One is the answer to this question:
Charge Q is placed on an infinitely thin conducting disk of radius R. How does it distribute itself over the disk?
The answer turns out to be that the charge distribution is the same as if you started with a uniform distribution of charge over a spherical shell, and compressed the shell down to a disk by smashing each piece of the surface straight up or down in the direction perpendicular to the disk.
Although I know of various proofs of this, particularly one provided by my friend and colleague Ovidiu Lipan, none of them seemed to me like a satisfying explanation of why the result was true. Of course, there might not be such a thing, but when the final answer has such a simple description (compared to most problems in E&M, which have incredibly messy solutions), it seems like there ought to be a nice reason for it.
Later I came across some notes by Kirk McDonald of Princeton provide a somewhat intuitive answer. I’ll summarize the idea here.
Start with something every E&M student should know. Take a spherical shell of radius R and thickness dR, and fill it uniformly with charge. Then the electric field inside the shell is zero. The slick way to prove this is with Gauss’s Law, but you can prove it with more basic geometric reasoning as follows. (In fact, I believe that the argument goes all the way back to Newton, although of course he wasn’t talking about electric fields, since they hadn’t been discovered / invented yet).
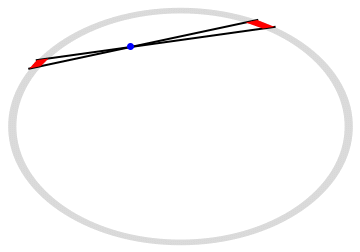
Say that you’re located at an arbitrary point inside the spherical shell. Draw two cones with infinitesimal solid angle going out in opposite directions. These intersect the shell giving two little “charge elements” shown in red below.
You can convince yourself that the electric field contributions from these charge elements exactly cancel each other. The volume, and hence the amount of charge, of each is proportional to the square of its distance from you, so by the inverse square law they give equal but opposite fields.
Since you can chop up the whole shell into such pairs, the total electric field vanishes.
The clever insight in McDonald’s notes is that the same argument holds even if you take the spherical shell and compress it into an ellipsoid (i.e., rescale all of the z coordinates by some constant factor, while leaving x and y the same):
With a bit of effort, you can convince yourself that all the various distances and volumes scale in such a way that the two field contributions remain equal and opposite.
Now that we know that the field inside this ellipsoid is zero, what can we conclude? First, take the limit as dR goes to zero, so we have a two-dimensional surface charge distribution. The result must be the same as the surface charge distribution on a solid, conducting ellipsoid. After all, the conducting ellipsoid has to have charge only on its surface and have zero field inside. The usual electrostatic uniqueness theorems apply here, which say that there’s only one charge distribution that leads to this result. Since we’ve found a charge distribution that does so, it must be the charge distribution.
Keep smashing the ellipsoid down until it lies in a plane, and you’ve got the solution for the conducting disk.

“(In fact, I believe that the argument goes all the way back to Newton, although of course he wasn’t talking about electric fields, since they hadn’t been discovered / invented yet).”
He was discussing gravity, of course. IIRC, he had an algebraic proof first but didn’t communicate the result because the fashion of the time valued geometric proofs more highly.
“The clever insight in McDonald’s notes is that the same argument holds even if you take the spherical shell and compress it into an ellipsoid”
Does it hold only for ellipsoids, or are there other shapes for which it holds as well? If the former, is there a proof? If the latter, what are they?
Good question. It’s not hard to convince yourself that it applies to all ellipsoids (including triaxial ellipsoids). I can’t see any way to generalize it beyond that, but I can’t say for sure that there aren’t generalizations. It’d be interesting if there were.
there is a simpler aproach to this problem.the equipotential surfuces for a uniform line charge are (in 2D) ellipses with foci on the ends of the line charge.so instead of an ellipsoid we put a rod with uniform charge( we put the corresponding rod which meets our conditions) then we have the potential every where outside the conducting ellipsoid( because we know how to do it for the rod).finally we calculate E on the surface and that gives us the surface charge density!
This seems like a great approach, but I can’t see how to make it work. I can see that this gives the charge distribution on any prolate spheroid (i.e., an ellipsoid with one long axis and two equal smaller axes), but I can’t see a way to use it to get the distribution on an oblate spheroid, which is what you need if you want to take the limit and get to a disk.
Am I missing something obvious?
Also, by the way, I don’t know what the parenthetical comment “in 2D” means. The equipotentials of the line of charge are spheroids in 3D, not 2D, right?
by 2D I meant 2D.you know its ellipse in 2D but we have symmetry which we rotate to get ellipsoid(and excuse me for my bad language,I dont know the exact world.) It is “prolate”.two of axes are equal.so we have an “2a” axis and two “2b” axises.if we take the limit as b approaches zero what do we get? a disk.so it gives the disk thing.and for your point on a general spheroid(three distinctive axes) I think we can again show that because of symmetry the additional phrase we get for the third axis will be similar to the two other.and we get the more general result as wanted.
by the way..thank you for reading my comment!
Maybe I’m just being stupid, but I still don’t get it. If you take the limit as b approaches zero, you have one long axis and two zero-length axes, which is a line, not a disk.
yepp.sorry..it was a typo…”a” should approach zero so that you get 2 axises “2b” which gives you a circle of radius “b”.right?
by the way…if we let “b” approach zero…that again answers a nice question..charge density on a conducting needle..which surprisingly gives constant charge density!!I’ve read an article on the needle thing…doing some computer work as well as analytical work..and then again this approach was still better than the approach the article(by jackson or griffiths I dont recall) had.
Sorry, but I’m still not getting it. The argument that you gave doesn’t allow you to take the limit a -> 0. The calculation of the potential due to a line of charge only gives you equipotential surfaces that are prolate spheroids (a>b), not oblate spheroids (a<b). To take the limit a -> 0 with fixed b, you’d need the latter.
You can find solutions to Laplace’s equation with oblate spheroidal equipotential surfaces by solving the equation in oblate spheroidal coordinates, if you like. In that coordinate system, Laplace’s equation is separable, and the solution that depends only on the “radial” coordinate is precisely the solution for the charged conducting disk. (Similarly, in prolate spheroidal coordinates, the solution that depends only on the radial coordinate is the one corresponding to a charged needle.) That’s another way of getting the solution for the disk, although I don’t think it’s intuitively satisfying in the way the smashed-spherical-shell solution is.
“Sorry, but I’m still not getting it. The argument that you gave doesn’t allow you to take the limit a -> 0. The calculation of the potential due to a line of charge only gives you equipotential surfaces that are prolate spheroids (a>b), not oblate spheroids (a< b). To take the limit a-> 0 with fixed b, you’d need the latter.”
I dont see why I cant let a->0.It works.in the calculations I never used that a>b .I cant really say that rigorously but for example in another (similar)problem I reached a radical for potential.in the radical I got a complex quantity.I guessed that because potential is real the answer would be th real part.and it came out correct.
here if we let a->0 we get the answer.I dont see whats the problem.you have a function of a.you take a limit .and get a valid answer.the laplacian solution might be more rigoros but I dont have a problem with this one either.
also:a similar problem to my “similar problem”:find potential of the disk in space? again if you take a->0 in my answer you get the correct answer.
So you’re saying that you take the solution from the charged line (which has prolate spheroidal equipotentials) and formally alter the parameters to make the spheroids oblate? I guess that’s fine. It’s perhaps a nicer way of getting the solution than some others. I thought at first that you were talking about a more physical connection between the charged-line problem and the charged-disk problem, as opposed to a formal mathematical manipulation.
(Not that there’s anything wrong with formal mathematical manipulations, of course!)
well intuitively I find this in a nice analogy with dipole.for a dipole we let q->0 and d->infinity such that qd->p.
now to get a disk as a equipotential in our example we should let the lenght of the charged rod aproach zero and its charge density aproach infinity such that their product approaches 2pie0VR.that V is the potential of the disk and R its Radius.(check the calculations though!)
by the way to prove that ellipses are equipotentials for a rod there are nice ways>>1)using the field and the property of ellipse.(about angles)2)finding the field lines for discrete charges on a rod.then take a limit and show it gives hyperbola.which are confocal to equipotential surfaces thus ellipses.3)findind V in space.putting it constant.(tricky algebra but simplifies with good choice of variables)